2Problem Analysis
Genetic algorithms represent a powerful optimization tool for many problem
domains. Hence, we expect that our system will be applied for a various
problems. The first characteristic feature of genetic algorithms is the
amount of parameters of the algorithm. The quality of the result and the
computational costs mostly depend on the individual parameters' setting,
specific to the solved problem. Unfortunately, we are not able to decide
what parameters' setting is optimal for any task. Therefore it is important
to support the maximum modularity of the algorithm i.e. to allow the user
to adjust the genetic algorithm to the solved problem. The second characteristic
feature of genetic algorithms is that they can be very time-consuming.
Hence, it would be useful to provide the user with tools for monitoring
the population and its quality and to allow him to adjust the parameters
of the genetic algorithm even during the computation. On the other hand,
it is important to support the long run of the genetic algorithm on the
background, without any interaction with the user.
We suppose that the users of our system have a different knowledge
of the topic. Therefore we provide them with various facilities
for adapting our system to their requirements. The degree of adaptation
varies from adjusting the supported parameters of the genetic algorithm
to rebuilding whole parts of the system. Every user has to describe the
solved problem before the run of the genetic algorithm. At first he has
to describe the form of individuals and their encoding to the genes. And
the second the user has to specify how to measure the quality of each individual
i.e. the user has to define the fitness function. If a neural network should
approximate the fitness function, then the user has to train it properly.
Any other additional input to the system is optional. For the input scheme
of genetic algorithm see Fig. 2-1.
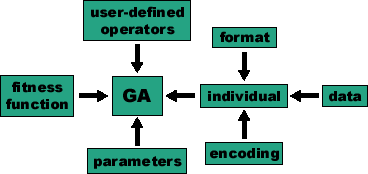
Figure 2-1: The scheme of input of genetic algorithm. The encoding and the format of the individual have to be specified. The individuals can be optionally initialized (initial data). The fitness function have to be defined by the user, to evaluate fitness value of an individual. The parameters of the computation must be set. Optionally special genetic operators can be defined by the user.
Our system consists of several relatively independent parts (components).
Except the system kernel providing the genetic algorithm itself, our system
contains supporting components. With these components the user can input and
adjust the genetic algorithm, and then he can control and monitor its run.
For an open system it is essential to define precisely the interfaces between
all its components. Then it is possible to replace any component by a new
one without any further change in the system. All the components are not implemented yet,
but our system is prepared for their incorporation (due the definition of interfaces).
The objective of the parallel approach to genetic algorithms is to reduce
the computational time of genetic algorithms and to enable a more extensive
search in the search space. It means to divide the computation to several
processors. It is important to choose the parallel method carefully to preserve
the overall performance of the genetic algorithm running on a single processor.
In addition, we expect a heterogeneous network of
workstations with a relatively slow communication. This fact handicaps
parallel methods based on a frequent communication.
Roughly speaking genetic algorithms proceed iteratively in two steps
during their run. First, they produce new genes using genetic operators
and afterwards they measure the fitness of all these new genes. Both steps
can be performed asynchronously and locally. This fact makes genetic algorithms
perspective for parallelization. There have been proposed several approaches
to parallel genetic algorithms. The first strategy deals with a single
global population that is shared by all processors. The drawbacks of this
approach consist in providing access to the population and in preserving
its consistency. Further methods divide the global population to many subpopulations.
In this case the proper information exchange between the subpopulations
must be provided. Otherwise the effect of parallelization would be lost.
The particular processors can be assigned to the subpopulations or even
to individuals. The last strategy assumes that the computation of the fitness
function value is very time-consuming. In such a case this value can be
computed in parallel way.
