Jednoduchý úvod do MATABu

Názov je skratka MATrix LABoratory Program navrhnutý na maticové výpočty pred viac než 20 rokmi

Contents

Hlavné použitie programu:

Absolútna väčšina funkcií MATLABu je implementovaná v GNU Octave. Octave je voľne šíriteľné vo verziách pre Unix (Linux) i pre Windows. Nemá grafické IDE. Nemá tooboxy. Kreslenie grafov nie je v Octave integrované. Typycky sa rieši pomocou GNU Plot.

Jednoduché výpočty

Ako vkladať čísla, vektory a matice a základné výpočty s nimi.

Základným dátovým typom sú n-rozmerné polia (primárne dvojrozmerné - matice) reálnych čísel. Zapisujú sa do hranatých zátvoriek. Oddeľovačom sú medzery, tabelátory a čiarky v riadkoch, stredníky znaky konca riadku oddeľujú riadky. Najprv vektory - riadkový x a stĺpcový y. Ich súčinom je matica. 

x=[2,3,4]

x =

     2     3     4


y=[1;2]

y =

     1
     2


z=y*x

z =

     2     3     4
     4     6     8


Vloženie matice
A=[2.3  4.8 9.2; 21.34 1.3e12 9]

A =

  1.0e+012 *

    0.0000    0.0000    0.0000
    0.0000    1.3000    0.0000

Pri výpise matice A je pred maticu vypísaný spoločný koeficient 1.0e+012 *, ktorým majú byť vynásobené všetky prvky matice 

B = [ 1 9 23
        21 2 1
        9 11 99]

B =

     1     9    23
    21     2     1
     9    11    99

Skaláry sú matice s rozmermi 1x1

a = 3.1

a =

    3.1000


u = a*z

u =

    6.2000    9.3000   12.4000
   12.4000   18.6000   24.8000

MATLAB rozlišuje veľké a malé písmená. Premenné sa nedeklarujú. Zoznam definovaných premenných sa zistí príkazom who

who

Your variables are:

A    C    E    T    ans  c    u    y    
B    D    I    a    b    d    x    z

Podrobnejšie informácie o premenných dá príkaz whos alebo okno Workspace

whos

  Name      Size            Bytes  Class      Attributes

  A         2x3                48  double               
  B         3x3                72  double               
  C         3x3                52  double     sparse    
  D         3x3                72  double               
  E         3x3                72  double               
  I         1x1                 8  double               
  T         2x2                 4  logical              
  a         1x1                 8  double               
  ans       1x1                 8  double               
  b         3x3                72  double               
  c         3x3                72  double               
  d         3x3                72  double               
  u         2x3                48  double               
  x         1x3                24  double               
  y         2x1                16  double               
  z         2x3                48  double

Aritmetika MATLABu je "robustná"

nekonecno = a/0

nekonecno =

   Inf


nula = 1 / nekonecno

nula =

     0


CoJeTo = nekonecno / nekonecno

CoJeTo =

   NaN

Vydrží aj odmocňovanie záporných čísel

sqrt(-1)

ans =

        0 + 1.0000i

MATLAB vie počítať s komplexnými číslami. Imaginárna jednotka sa značí buď i alebo j

(1+2i)*(1-2j)

ans =

     5

MATLAB je vlastne veľmi výkonná kalkulačka. Výsledok posledného výrazu (neuloženého do premennej) je v premennej ans

2^3

ans =

     8


2^4

ans =

    16


2^100

ans =

  1.2677e+030


20^3-3*23/8

ans =

  7.9914e+003


sqrt(ans)

ans =

   89.3945

Ovláda mnoho aritmetických funkcií:

sin(4)

ans =

   -0.7568


sin(3*pi)+cos(1.23)^2

ans =

    0.1117


log(2430)

ans =

    7.7956

Aký základ používa funkcia log? Pomôže nám nápoveda 

help log

 LOG    Natural logarithm.
    LOG(X) is the natural logarithm of the elements of X.
    Complex results are produced if X is not positive.
 
    See also LOG1P, LOG2, LOG10, EXP, LOGM, REALLOG.

    Reference page in Help browser
       doc log

Dokonalejšia nápoveda je hypertextová nápoveda prístupná cez tlačítko Start > Help alebo cez tlačítko so znakom '?' v modrom krúžku na toolbare pod menu. O funkciách sa dá ľahko zistiť nápoveda cez tlačítko fx vedľa promptu v príkazovom okne Command Window. Ďalšími možnosťami sú demo-videa a demo príklady.

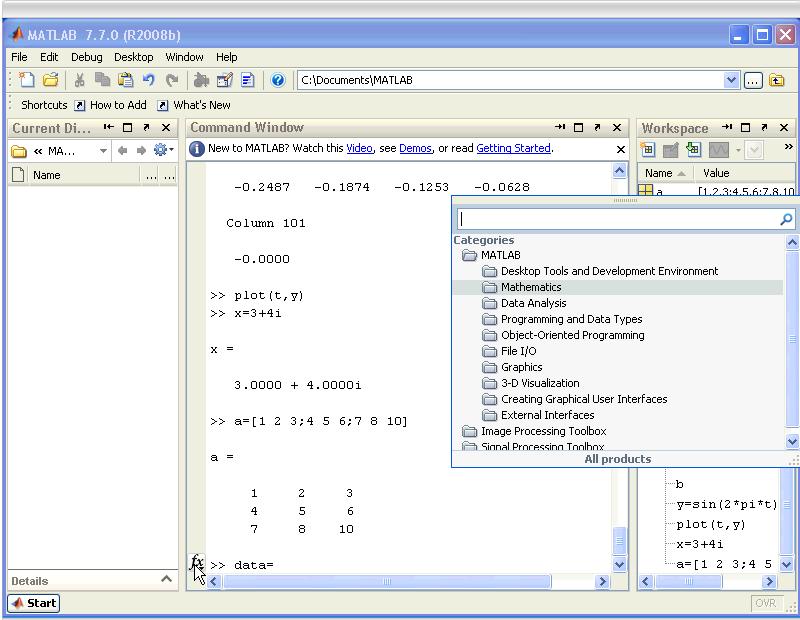
Aritmetické operácie s maticami

Bežné aritmitecké operácie ale i delenie maticou!

Štandardné operácie

Ak výraz končí bodkočiarkou ';', tak sa jeho výsledok nezobrazí. Sčítanie, odčítanie

A = [1 2 3; 2 3 1; 0 7 3];
B = [1 1 1; 3 2 1; 7 6 5];
C = [3 3; 3 3; 4 3];
whos

  Name           Size            Bytes  Class      Attributes

  A              3x3                72  double               
  B              3x3                72  double               
  C              3x2                48  double               
  CoJeTo         1x1                 8  double               
  D              3x3                72  double               
  E              3x3                72  double               
  I              1x1                 8  double               
  T              2x2                 4  logical              
  a              1x1                 8  double               
  ans            1x1                 8  double               
  b              3x3                72  double               
  c              3x3                72  double               
  d              3x3                72  double               
  nekonecno      1x1                 8  double               
  nula           1x1                 8  double               
  u              2x3                48  double               
  x              1x3                24  double               
  y              2x1                16  double               
  z              2x3                48  double               


A+B

ans =

     2     3     4
     5     5     2
     7    13     8


A-B

ans =

     0     1     2
    -1     1     0
    -7     1    -2

Príkaz A+C; spôsobí chybové hlásenie

Error using ==> plus

Matrix dimensions must agree.

Maticové násobenie:

D = A*C

D =

    21    18
    19    18
    33    30


A*B

ans =

    28    23    18
    18    14    10
    42    32    22


B

B =

     1     1     1
     3     2     1
     7     6     5

Násobenie skalárom:

3*B

ans =

     3     3     3
     9     6     3
    21    18    15

Násobenie po zložkách .*: 

A.*B

ans =

     1     2     3
     6     6     1
     0    42    15

Transpozícia matice

Pre maticu reálnych čísel A je A' transponovaná matica k matici A. 

A = [ 1 2 3; 4 5 6]

A =

     1     2     3
     4     5     6


A'

ans =

     1     4
     2     5
     3     6

V skutočnosti je A' matica (komplexne) konjugovaná k matici A, to znamená, že ak A obsahuje komplexné čísla s nenulovou imaginárnou časťou, tak po transpozícii sú u imainárnych častí opačné znamienka 

B = A+i*(rand(2,3)-0.5)

B =

   1.0000 + 0.1557i   2.0000 + 0.3491i   3.0000 + 0.1787i
   4.0000 - 0.4643i   5.0000 + 0.4340i   6.0000 + 0.2577i


B'

ans =

   1.0000 - 0.1557i   4.0000 + 0.4643i
   2.0000 - 0.3491i   5.0000 - 0.4340i
   3.0000 - 0.1787i   6.0000 - 0.2577i

Ak aj v prípade komplexných čísel potrebujeme iba transponovanú maticu bez zmeny znamienok, tak sa pred apostrof vloží bodka:

B.'

ans =

   1.0000 + 0.1557i   4.0000 - 0.4643i
   2.0000 + 0.3491i   5.0000 + 0.4340i
   3.0000 + 0.1787i   6.0000 + 0.2577i

Generovanie matíc

zeros(m,n) je nulová matica mxn

zeros(2,3)

ans =

     0     0     0
     0     0     0

ones(m,n) je matica mxn obsahujúca samé jedničky 

ones(2,3)

ans =

     1     1     1
     1     1     1

eye(n) je jednotková matica nxn

eye(3)

ans =

     1     0     0
     0     1     0
     0     0     1

diag(v) je diagonálna matica, ktorá je nulová a na diagonále sú prvky z vektora v

diag([1,2,3])

ans =

     1     0     0
     0     2     0
     0     0     3

Riešenie sústavy lineárnych rovníc "delením maticou"

Ak matica A nie je singulárna, tak sústava rovníc

$$Ax=b$$

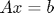
má riešenie

$$x=A^{-1}b$$

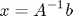
V MATLABe je na to operátor "delenia zľava" vo forma opačného lomítka. Najprv vygeneruyjeme náhodnú maticu A

A=rand(3,3)

A =

    0.7431    0.1712    0.2769
    0.3922    0.7060    0.0462
    0.6555    0.0318    0.0971

Náhodný vektor b

b=rand(3,1)

b =

    0.8235
    0.6948
    0.3171

Potom sústavu

$$Ax=b$$

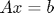
vyriešime:

x=A\b

x =

    0.1268
    0.7727
    2.1556

Výsledok (získaný iteratívnou numerickou metódou) skontrolujeme:

A*x-b

ans =

     0
     0
     0

Generovanie vektorov

Pre rôzne účely sú často treba vektory reprezentujúce lineárne a iné typy postupností.

Rastúca postupnosť celých čísel od A do B sa vygeneruje zápisom A:B

t = 1:6

t =

     1     2     3     4     5     6


Jedná sa o aritmetickú postupnosť, veľkosť kroku môže byť ľubovoľná
|A:Krok:B|
t=-1:0.2:1

t =

  Columns 1 through 6

   -1.0000   -0.8000   -0.6000   -0.4000   -0.2000         0

  Columns 7 through 11

    0.2000    0.4000    0.6000    0.8000    1.0000

Aj negatívny krok je možný

t = 20:-3:1

t =

    20    17    14    11     8     5     2

Podobne funguje funkcia linspace(A,B,N), ktorá vráti N čísel, ktoré interval

$$<|A|,|B|>$$

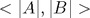
rozdelia rovnomerne na N-1 dielikov. 

linspace(0,1,11)

ans =

  Columns 1 through 6

         0    0.1000    0.2000    0.3000    0.4000    0.5000

  Columns 7 through 11

    0.6000    0.7000    0.8000    0.9000    1.0000

Logaritmickú postupnosť medzi 10^A a 10^B generuje funkcia logspace(A,B,N)

logspace(1,6,7)

ans =

  1.0e+006 *

  Columns 1 through 6

    0.0000    0.0001    0.0005    0.0032    0.0215    0.1468

  Column 7

    1.0000

Vektorizované funkcie

Pokiaľ je to zmysluplné, tak všetky funkcie v MATLABe sú tzv. vektorizované. To znamená, že je možné im ako agument dať vektor a výsledkom bude aplikácia funkcie na každý prvok vektora. Napríklad tabuľka funkcie sin(2t) na intervale

$$ <0 ,\pi>$$

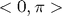
 t = 0:0.1:pi

t =

  Columns 1 through 6

         0    0.1000    0.2000    0.3000    0.4000    0.5000

  Columns 7 through 12

    0.6000    0.7000    0.8000    0.9000    1.0000    1.1000

  Columns 13 through 18

    1.2000    1.3000    1.4000    1.5000    1.6000    1.7000

  Columns 19 through 24

    1.8000    1.9000    2.0000    2.1000    2.2000    2.3000

  Columns 25 through 30

    2.4000    2.5000    2.6000    2.7000    2.8000    2.9000

  Columns 31 through 32

    3.0000    3.1000


tab = sin(2*t)

tab =

  Columns 1 through 6

         0    0.1987    0.3894    0.5646    0.7174    0.8415

  Columns 7 through 12

    0.9320    0.9854    0.9996    0.9738    0.9093    0.8085

  Columns 13 through 18

    0.6755    0.5155    0.3350    0.1411   -0.0584   -0.2555

  Columns 19 through 24

   -0.4425   -0.6119   -0.7568   -0.8716   -0.9516   -0.9937

  Columns 25 through 30

   -0.9962   -0.9589   -0.8835   -0.7728   -0.6313   -0.4646

  Columns 31 through 32

   -0.2794   -0.0831

Graf tejto funkcie potom môžeme jednoducho zobraziť

plot(t,tab)

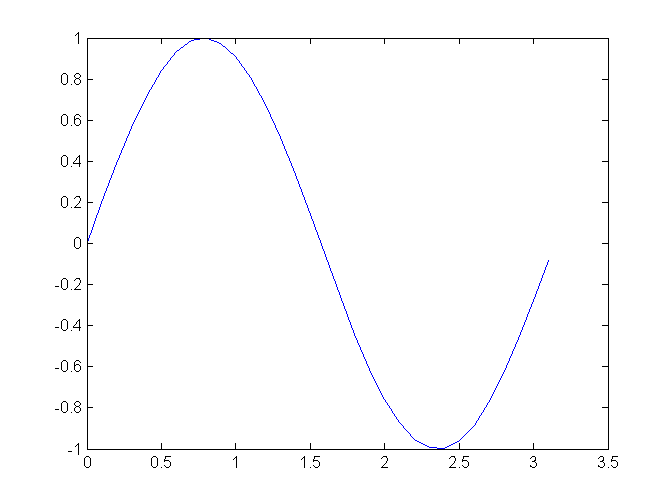
Pozor na násobenie a umocňovanie. Typicky potrebujeme výpočet po zložkách. Príklad: výpočet funkcie

$$1/(1+x^2)$$

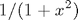
x = -2:0.1:2;
y = 1./(1+x.^2);
plot(x,y)

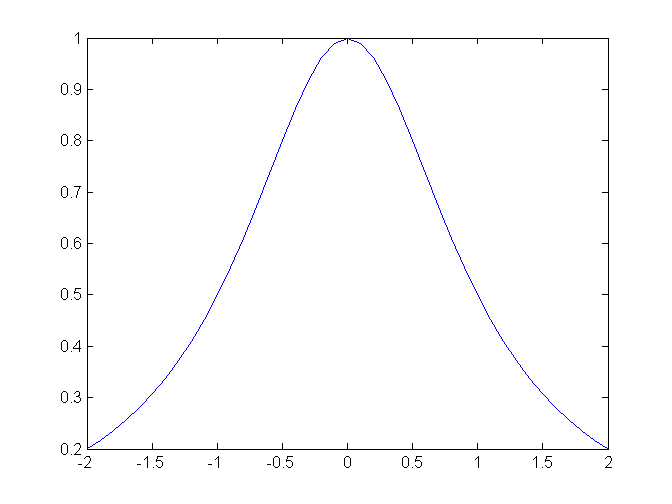
Kreslenie grafov

MATLAB umožňuje kresliť 2D i 3D grafy. Už sme videli kreslenie 2D grafu pomocou funkcie plot(x,y). Táto funkcia je rozšírená. Tretí parameter udáva paremetre zobrazenia grafu. Napríklad farbu grafu - červený graf: 

plot(x,y,'r')

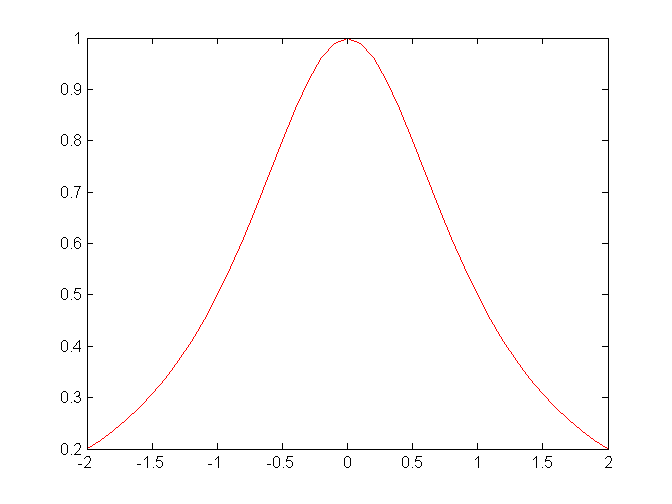
Zelený graf čiarkovaný:

plot(x,y,'g--')

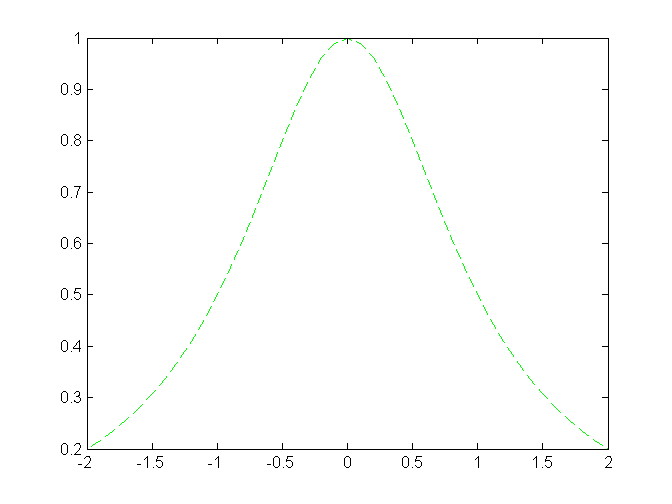
Bez spojovania zobrazených bodov. Body v tvare krúžkov:

plot(x,y,'o')

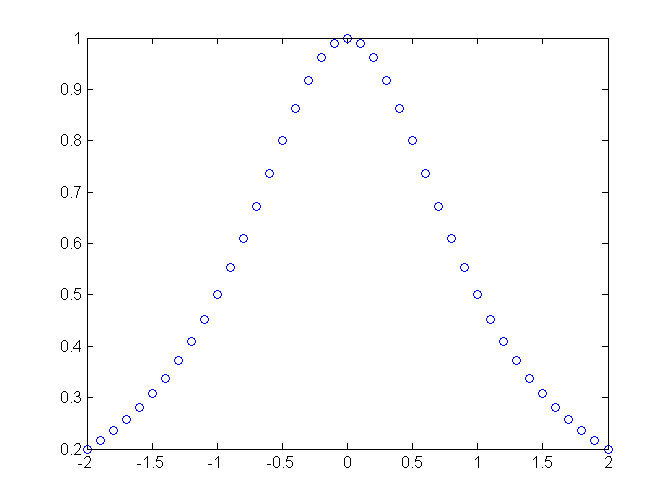
Bez spojovania zobrazených bodov. Body v tvare krížikov:

plot(x,y,'+')

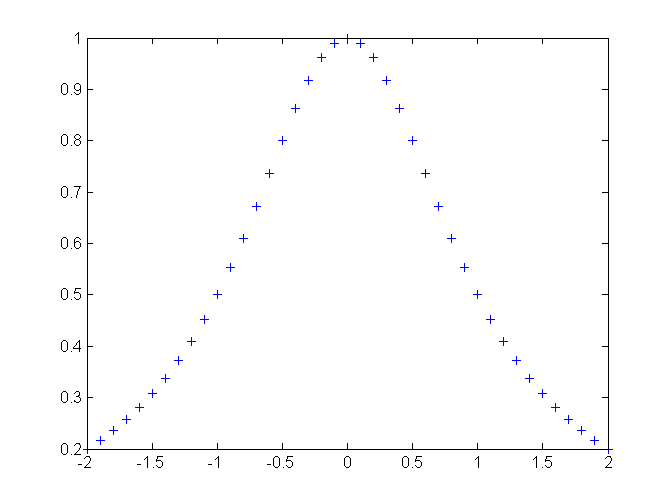
Ďalšie možnosti viz nápoveda funkcie plot.

Popisy grafu je možné meniť. xlabel('string') a ylabel('string') zmenia popisy x-ovej a y-ovej osy grafu. 

xlabel('x hodnoty');
ylabel('1/(1+x^2)');
plot(x,y)

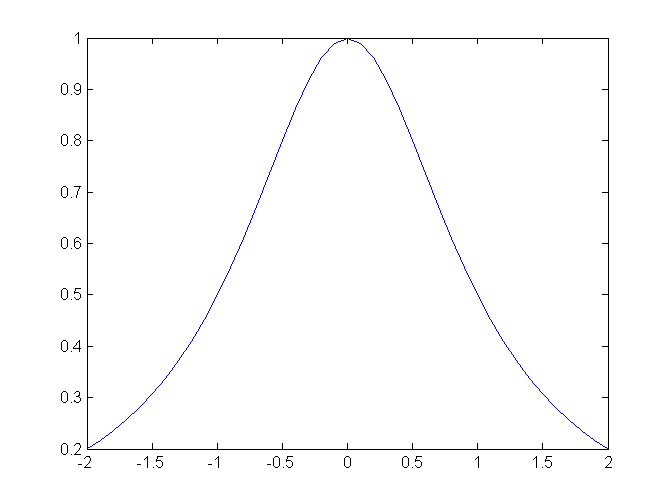
grid pridá do grafu pravouhlú mriežku. hold on "podrží" graf a dovolí pridávať do obrázku grafy ďalších funkcií 

hold on
plot(x,sin(x))

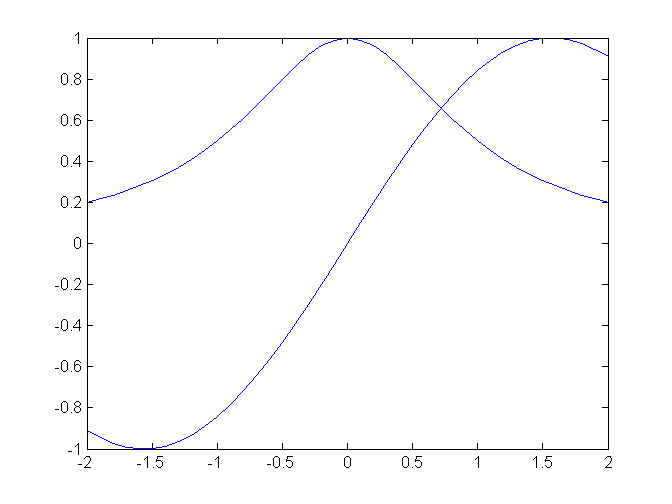
hold off ukončí "držanie" grafu. 

hold off

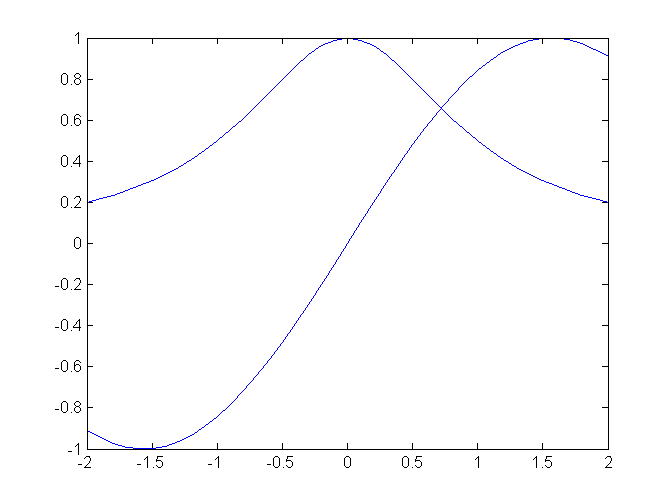
Viacej grafov je možné nakresliť aj pridaním ďalších parametrov do volania plot. 

plot(x,y,'r+--',x,sin(x),'go:')

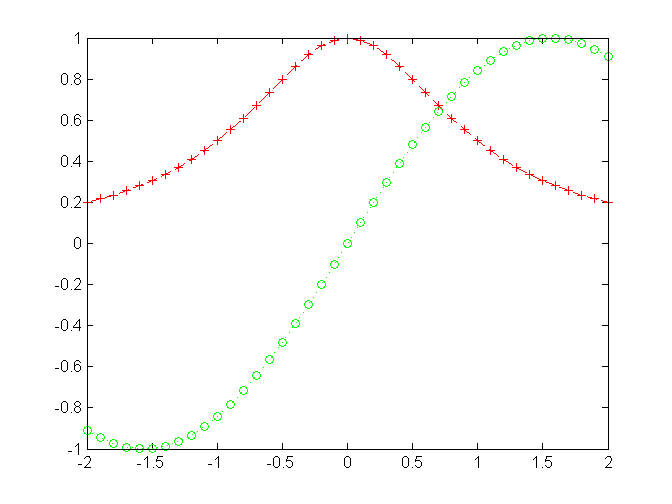
Ďalšie užitočné príkazy

max(x) v prípade, že x je vektor, tak je to jeho maximálny prvok. Ak je x matica, tak vráti maximálne prvky v jednotlivých stĺpcoch. Ďalšie možnosti sú popísané v nápovede. 

x

x =

  Columns 1 through 6

   -2.0000   -1.9000   -1.8000   -1.7000   -1.6000   -1.5000

  Columns 7 through 12

   -1.4000   -1.3000   -1.2000   -1.1000   -1.0000   -0.9000

  Columns 13 through 18

   -0.8000   -0.7000   -0.6000   -0.5000   -0.4000   -0.3000

  Columns 19 through 24

   -0.2000   -0.1000         0    0.1000    0.2000    0.3000

  Columns 25 through 30

    0.4000    0.5000    0.6000    0.7000    0.8000    0.9000

  Columns 31 through 36

    1.0000    1.1000    1.2000    1.3000    1.4000    1.5000

  Columns 37 through 41

    1.6000    1.7000    1.8000    1.9000    2.0000


max([2, -33.1,14,9])

ans =

    14


A

A =

    0.7431    0.1712    0.2769
    0.3922    0.7060    0.0462
    0.6555    0.0318    0.0971


max(A)

ans =

    0.7431    0.7060    0.2769

Podobne funguje min(x).

abs(x) počíta absolútnu hodnotu prvkov z x. 

abs([1, -3,-4, 2])

ans =

     1     3     4     2

size(x) vráti vektor s rozmermi matice x v jednotlivých dimenziách 

size(D)

ans =

     3     2

length(x) vráti "dĺžku" poľa x, tj. max(size(x)). 

length(D)

ans =

     3

save fname uloží stav všetkých definovaných premenných do súboru fname.mat

save 'h:\Data Mining\MatLab\Tst.mat'

save fname var1 var2 uloží iba obsahy vymenovaných premenných

load fname načíta obsah premenných zo súboru fname.mat.

quit ukončí MATLAB

Práca s prvkami matíc

C

C =

     3     3
     3     3
     4     3


C(2,1)

ans =

     3

Druhý riadok matice C

C(2,:)

ans =

     3     3

Druhý a tretí riadok matice C

C(2:3,:)

ans =

     3     3
     4     3

Prvý stĺpec matice C

C(:,1)

ans =

     3
     3
     4

Vybrané prvky vektora

x=0:2:14

x =

     0     2     4     6     8    10    12    14


idx = [ 3 1 4];
x(idx)

ans =

     4     0     6

Takéto indexovanie je možné využiť i na zmenu prvkov v matici (vektore)

x(idx)=[1,2,3]

x =

     2     2     1     3     8    10    12    14

Formát výstupu

Štandardne MATLAB vypisuje čísla na obmedzený počet platných číslic (5) a medzi riadky výstupu vkladá často prázdne riadky. To sa dá zmeniť. Väčší počet platných číslic získame príkazom 

format long
A

A =

   0.743132468124916   0.171186687811562   0.276922984960890
   0.392227019534168   0.706046088019609   0.046171390631154
   0.655477890177557   0.031832846377421   0.097131781235848

Je možné si vynútiť exponenciálny tvar zápisu čísel

format long e
A

A =

  Columns 1 through 2

    7.431324681249162e-001    1.711866878115618e-001
    3.922270195341682e-001    7.060460880196088e-001
    6.554778901775566e-001    3.183284637742068e-002

  Column 3

    2.769229849608900e-001
    4.617139063115394e-002
    9.713178123584754e-002

Alebo krátky zápis v exponenciálnom tvare

format short e
A

A =

  7.4313e-001  1.7119e-001  2.7692e-001
  3.9223e-001  7.0605e-001  4.6171e-002
  6.5548e-001  3.1833e-002  9.7132e-002

Alebo krátky zápis bez vynúteného exponenciálneho tvaru - ak je to nutné, tak sa exponenciálny tvar použije, inak nie

format short
A

A =

    0.7431    0.1712    0.2769
    0.3922    0.7060    0.0462
    0.6555    0.0318    0.0971

Ale za najužitočnejšie považujem možnosť vynechať zbytočné prázdne riadky na výstupe a výstup "skompaktniť"

format compact
A

A =
    0.7431    0.1712    0.2769
    0.3922    0.7060    0.0462
    0.6555    0.0318    0.0971

Ďalšie možnosti - budú predstavené na ďalšom cvičení

Úloha

Nakreslite "žblunknutie kameňa do vody" ako 3D-graf funkcie dvoch premenných. Vlny by sa mohli počítať ako sin(vzdialenosť od počiatku súradníc). So vzdialenosťou od počiatku súradníc by výška vĺn mala klesať.


Published with MATLAB® 7.7