We can use recursion to solve many problems of a combinatorial nature, such as generating subsets, combinations, or permutations of a set. As we solve these problems we can use recursion to explore a tree of possibilities.
As a first example, suppose that we'd like to
write a function that
takes an integer n and
prints out all possible strings of length n containing only
characters from the set {'a', 'b', 'c'}.
For example, if n = 2 then we
will print these strings:
aa ab ac ba bb bc ca cb cc
And if n = 3:
aaa aab aac aba abb abc aca acb acc baa bab bac …
There will be 3n strings in the output list. That's because there are 3 possible choices for the first letter, 3 for the second letter, and so on for each of the n letters.
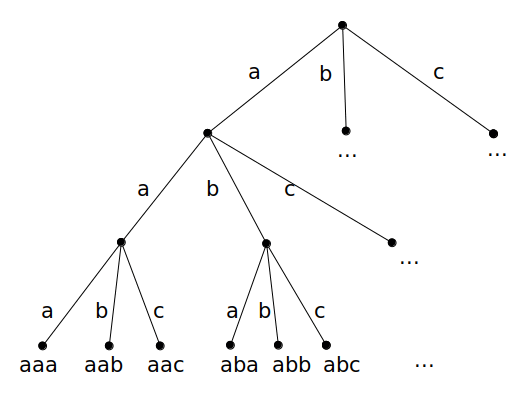
We can imagine a series of choices that we must make as we choose a string to print out. We can draw these in a tree. For example, if n = 3:

At each step, we choose the letter 'a', 'b' or 'c'. Affter we have made N choices, we have a string that we can print.
We can use recursion to descend this tree. At each level of the tree, we'll make three recursive calls, one for each choice that we can make (a, b, or c). As we descend the tree, we will remember all choices that we have made so far. We can accomplish that in several different ways, each of which will lead to a slightly different solution. As we'll see below, a non-recurisve solution to this problem is also possible.
As the recursion descends, we can accumulate choices into a prefix string that we pass to each recursive call. When we have made N choices, we have reached a leaf of the tree and will print out the string we have built.
Here is our solution:
void print(string s) => Console.WriteLine(s);
void abc(int n) {
void go(string prefix) {
if (prefix.Length == n)
print(prefix);
else
foreach (char c in "abc")
go(prefix + c);
}
go("");
}As another possibility, we can store all choices in an array. Our solution will look like this:
void abc2(int n) {
char[] a = new char[n];
void go(int i) {
if (i == n)
print(string.Join("", a));
else
foreach (char c in "abc") {
a[i] = c;
go(i + 1);
}
}
go(0);
}As yet another possibility, as the recursion descends we can push all choices we've made so far onto a stack. Once we have made N choices, we can print out the values on the stack. Each time the recursion returns, we pop our last choice off the stack, restoring its previous state. This solution might look like this:
void abc3(int n) {
Stack<char> stack = new();
void go(int i) {
if (i == n)
print(string.Join("", stack.Reverse()));
else
foreach (char c in "abc") {
stack.Push(c);
go(i + 1);
stack.Pop();
}
}
go(0);
}
We call the Linq method Reverse() above so that we print
out characters in the order we chose them. For example, if we choose
'b', then 'a', then 'c', then iterating over the stack will produce
the values 'c', 'a', and 'b' in that order. Reversing produces the
order 'b', 'a', 'c'.
In solution 1 above, we never have to undo a choice that we have made, because the expression 'prefix + c' creates a copy of the prefix string with the additional character c. The original prefix string remains unchanged (as it must be, since strings are immutable in C#). However, this stack-based solution may be slightly more efficient because it never copies the set of choices accumulated so far.
When we study larger problems that explore an exponential state space, we will often see this same choice: we may either (a) copy the state each time we recurse, or (b) modify the state before recursing, then undo the change afterwards.
We can actually solve this problem non-recursively, by extracting digits from an integer. To see how this will be possible, suppose that instead of the characters 'a', 'b' and 'c' we want to generate the digits 0, 1, and 2. Then our output for N = 3 will look like this:
000 001 002 010 011 012 020 021 022 100 101 …
This is simply all 3-digit numbers in base 3!
For a given N, there are 3N N-digit numbers in base 3, which is exactly the number of possible solutions that we saw before. So we may simply loop through integers from 0 to 3N – 1, extract a series of base-3 digits from each, and convert each such digit to a character 'a', 'b' or 'c'. Here is a possible solution:
void abc3(int n) {
string convert(int i) {
string s = "";
for (int k = 0 ; k < n ; ++k) {
s = "abc"[i % 3] + s;
i = i / 3;
}
return s;
}
int p = (int) Math.Pow(3, n);
for (int i = 0 ; i < p ; ++i)
print(convert(i));
}Another typical combinatorial problem is generating all subsets of a set. Specifically, suppose that for any N we'd like to generate all subsets of the set {1, 2, …, N}. For N = 3, our output might look like this (in some order):
{ }
{ 1 }
{ 2 }
{ 1 2 }
{ 3 }
{ 1 3 }
{ 2 3 }
{ 1 2 3 }One way to view this problem is as a series of N choices, one for each of the values {1, 2, …, N}. In each choice, we decide whether a certain value will be absent from the set or present in it. Each of these N choices is a binary decision, and so there will be 2N possible solutions.
We can solve this problem using any of the techniques that we saw above for the abc problem. Let's write a solution using a prefix parameter:
void subsets(int n) {
void go(string prefix, int i) {
if (i > n)
print("{" + prefix + "}");
else {
go(prefix + i + " ", i + 1); // i is in the subset
go(prefix, i + 1); // i is not in the subset
}
}
go(" ", 1);
}Our decisions are binary, so our recursive function calls itself twice, once for each possible choice.
Let's run it:
subsets(3);
This will produce this output:
{ 1 2 3 }
{ 1 2 }
{ 1 3 }
{ 1 }
{ 2 3 }
{ 2 }
{ 3 }
{ }As another possible approach, at every recursive step we can either choose the next value that will be in the subset, or decide that there will be no more values and so the subset is complete. That leads to a solution that looks like this:
void subsets2(int n) {
void go(string prefix, int i) {
print("{" + prefix + "}"); // add no more values
for (int j = i ; j <= n ; ++j)
go(prefix + j + " ", j + 1); // add value j and recurse
}
go(" ", 1);
}Let's run it:
subsets(3);
This will produce the same subsets as the previous solution, but in a somewhat different order:
{ }
{ 1 }
{ 1 2 }
{ 1 2 3 }
{ 1 3 }
{ 2 }
{ 2 3 }
{ 3 }As another example of a combinatorial problem, consider Czech coins, which have the following denominations: 1 Kč, 2 Kč, 5 Kč, 10 Kč, 20 Kč, 50 Kč. Suppose that we'd like to print out all possible ways of forming a sum N using Czech coins. For the moment, let's assume that order matters, e.g. 1 + 2 and 2 + 1 are distinct sums.
We can solve this problem using recursion. Here is a possible solution, using a stack to remember the choices we have made:
int[] coins = { 1, 2, 5, 10, 20, 50 };
void sum(int n) {
Stack<int> nums = [];
// Add coins to make the remaining sum (rem).
void go(int rem) {
if (rem == 0)
print(string.Join(" + ", nums.Reverse()));
else
foreach (int c in coins)
if (c <= rem) {
nums.Push(c);
go(rem - c);
nums.Pop();
}
}
go(n);
}
Our recursive helper function go() takes an integer rem
indicating the remaining sum that we need to form. If rem
is 0, we have found a solution, so we print out the string. Otherwise
we recurse once for every possible coin size that is less than or
equal to rem, subtracting it from the remaining sum that
we need to form.
The call sum(5) will produce this
output:
1 + 1 + 1 + 1 + 1 1 + 1 + 1 + 2 1 + 1 + 2 + 1 1 + 2 + 1 + 1 1 + 2 + 2 2 + 1 + 1 + 1 2 + 1 + 2 2 + 2 + 1 5
Now suppose that order does not matter - for example, 1 + 2 and 2 + 1 are considered to be the same sum, so we only want to print one of these. How can we achieve this? In theory we could use the previous function to generate all possible sums, then somehow filter out duplicates, but that would be extremely inefficient since each sum can be permuted in many possible ways. Instead, let's modify our code so that it only considers sums in which integers appear in non-increasing order. For example, if N = 10 then it will print 5 + 2 + 2 + 1, but not any other permutation of these numbers.
We can accomplish this by making a small change to
our recursive helper function: it will take an extra argument max
indicating the maximum value of any coin which may be chosen at any
future point on the current branch of the decision tree. For example,
after we have chosen the coins 5 and 2, we will pass max
= 2 so that any coin chosen after that cannot be more than 2. That
will force each solution to be non-increasing. Here is the modified
code:
int[] coins = { 1, 2, 5, 10, 20, 50 };
void sum(int n) {
Stack<int> nums = [];
// Only use coins of size <= max.
void go(int rem, int max) {
if (rem == 0)
print(string.Join(" + ", nums.Reverse()));
else
foreach (int c in coins)
if (c <= rem && c <= max) {
nums.Push(c);
go(rem - c, c);
nums.Pop();
}
}
go(n, n);
}
The call sum2(5) will produce this output:
1 + 1 + 1 + 1 + 1 2 + 1 + 1 + 1 2 + 2 + 1 5
We can solve a large number of problems using an exhaustive search. This means that we search through a problem space, looking for solutions - typically those which satisfy various constraints.
Typically our search will be recursive, so it will explore a tree of possibilities. However the shape of this tree may be different than in the combinatorial problems we saw above, because some parts of the tree will be cut off. That's because as we explore the tree, at some points there may be no decision we can make that will satisfy the problem's constraints. So at that point the search will backtrack and explore the next possibility. This approach is sometimes called a backtracking depth-first search.
A classic example of a problem that we can solve in this way is the N queens puzzle. Our goal is to place N queens on a chessboard such that none of them attack any other. Recall that queens in chess may move horizontally, vertically, or diagonally.
A moment's reflection will show that the puzzle has a trivial solution for N = 1, and no possible solutions for N = 2 or N = 3. Now let's think about how to search for a solution for N = 4.
Certainly we may only place one queen in any row. And, since we must place N queens, every row will need to contain a queen. So in this problem the first decision we may make is where to place the queen in the first row. After that, we can decide where to place the queen in the second row, and so on. As we explore this tree of possibilities, we will not consider all possible ways to place N queens in N rows (there are NN of those) since the search will only explore parts of the tree where all queens placed so far satisfy the constraints, i.e. don't attack each other.
Here is a partial search tree for N = 4:
In the leftmost two branches of this tree, the search gets cut off because there is no valid position in which to place a queen in the next row. The third branch leads to a solution. If we allow our search to continue past that point, it will find one more solution (which is a rotated version of this one).
One easy way to write this search in
C# is to use a stack that holds the positions of all the queens
placed so far. We'll define a type Pos that holds an (x,
y) pair which is the position of a single queen. Here is our
solution:
using static System.Console;
using static System.Math;
using Pos = (int x, int y);
// Return true if queens at the given positions attack each other.
bool attack(Pos p, Pos q) =>
p.x == q.x || p.y == q.y || Abs(p.x - q.x) == Abs(p.y - q.y);
void print_board(int n, Stack<Pos> queens) {
for (int y = 0 ; y < n ; ++y) {
for (int x = 0 ; x < n ; ++x)
Write(queens.Contains((x, y)) ? "Q " : ". ");
WriteLine();
}
WriteLine();
}
void queens(int n) {
Stack<Pos> queens = [];
void go(int y) {
if (y == n) {
print_board(n, queens);
return;
}
for (int x = 0; x < n ; ++x)
if (!queens.Any(q => attack((x, y), q))) {
queens.Push((x, y));
go(y + 1);
queens.Pop();
}
}
go(0);
}Let's run this function to find a solution for N = 12. The call
queens(12);
produces this output as the first solution it finds:
Q . . . . . . . . . . . . . Q . . . . . . . . . . . . . Q . . . . . . . . . . . . . . Q . . . . . . . . . . . . . Q . . . . . . . . . . . . . Q . . . . . Q . . . . . . . . . . . . . . . . Q . . Q . . . . . . . . . . . . . . . . Q . . . . . . . . . . . . . Q . . . . . . Q . . . . . . . .
We may often want to plot data that a program has produced. For plotting in C# I recommend the ScottPlot library. Like Python's matplotlib, it lets you generate plots in just a few lines of code. To add ScottPlot to your C# project, type
$ dotnet add package ScottPlot
Our C# library quick reference lists some ScottPlot methods that should be adequate for simple plots.
As an example, let's write a program that displays
a histogram of the lengths of words in War and Peace. We can easily
read all lines in the file, split them into words and count the words
of each length. After that, we can use ScottPlot's Bars()
method to add histogram bars. Here is the code:
using ScottPlot;
Dictionary<int, int> count = [];
foreach (string line in File.ReadLines("war_and_peace"))
foreach (string word in line.Split())
if (word.Length >= 1)
count[word.Length] = count.GetValueOrDefault(word.Length) + 1;
Plot plot = new();
plot.Add.Bars(count.Keys.Select(k => (double) k), count.Values);
plot.SaveSvg("words.svg", 800, 800);The basic ScottPlot package cannot display graphics, but it can save a plot to a file, so we've done that in our program. (There are other ScottPlot packages that can display graphics in various ways, though they may not all work on all platforms.) Here is the plot our program produces: