
Write a program that simulates a random walk in two dimensions. The program should take an integer N on the command line, and simulate N random steps starting from the origin (0, 0). Each step should move randomly left, right, up, or down. The program should print the position after each random step. At the end, it should print the number of times that the walk visited the origin, and also the furthest Manhattan distance (|x| + |y|) that was reached from the origin. For example:
$ runghc walk 10 0 0 0 1 1 1 1 2 0 2 0 1 1 1 1 0 0 0 0 1 0 2 visits to origin: 2 furthest distance: 3
a) Write a function toArray :: [a] ->
Array Int a that converts a list to an array with integer
indices, indexed from 0.
b) Write a function array2d :: [[a]] ->
Array (Int, Int) a that converts a list of lists to a
2-dimensional array with integer indices, indexed from 0.
Write a function isPerm :: [Int] → Bool
that takes a list of N integers and returns True if the list holds
some permutation of the integers 1, .., N.
Write a function partition :: [Int] ->
Maybe ([Int], [Int]) that takes a list of integers and
determines whether it can be partitioned into two sets whose sum is
equal. If so, the function should return a Just with two lists
containing the numbers in each set. If not, it should return Nothing.
Write a function csort :: (Int, Int) ->
[Int] -> [Int] that implements a counting sort.
(csort (lo, hi) xs) should sort a list xs of values, all
of which are in the range lo ≤ x ≤ hi. It should run in O(N),
where N = length xs.
Implement a radix sort. Given any base d, your function should be able to sort N numbers in the range 1 .. R in time O(N · logd(R)), using much less memory than a counting sort.
Define a type IMap
a that is a map from a fixed
range of integers (indexed from 0) to values of type a.
Provide the following functions:
makeIMap :: [a] -> IMap a iget :: IMap a -> Int -> a iset :: IMap a -> Int -> a -> IMap a
makeIMap can assume that the given list is non-empty.
The iget and iset functions should run in
O(log N), where N is the number of elements in the map.
Also declare that IMap is an instance
of Functor.
Consider the game of Rock, Paper, Scissors. Two players choose their moves simultaneously. Paper beats rock; rock beats scissors; scissors beats papers. Suppose that two players will play a series of games. A strategy for this game is a function which chooses a move, given all moves that the opponent has played before:
data Move = Rock | Paper | Scissors type Strategy = [Move] → Move
Assume that in the list of moves given to a Strategy, the most recent move appears first.
a) Write a Strategy that plays whatever will beat the opponent's last move.
b) Write a Strategy that chooses the move that the opponent has played most often in the past, and plays whatever will beat that.
c) Write a Strategy that ignores the opponent's moves and plays Rock, then Paper, then Scissors, then Rock…
d) Write a function play :: Int → Strategy
→ Strategy → IO () that simulates a given number of games
between two strategies. It should produce output that looks like
this:
game 1: p1 = Paper, p2 = Scissors (p2 wins) game 2: p1 = Rock, p2 = Rock (draw) game 3: p1 = Rock, p2 = Paper (p2 wins) total: p1 won 0, p2 won 2, 1 draw
Fox and Hounds is a two-player game played on the black squares of an 8 x 8 chessboard:

One player controls a single fox, and the other controls four hounds. On the fox's turn, he can move one square in any direction diagonally. On the hounds' turn, one hound can move one square diagonally forward. The fox moves first. If the fox reaches the last row, he wins. If any player is ever unable to move, they lose.
a) Create a type Game representing
the state of this game. Also create a value start :: Game
representing the initial state of the game.
b) Write a function show_game :: Game →
String that produces a visual representation of the board:
> putStr (show_game start) H H H H . . . . . . . . . . . . . . . . . . . . . . . . F . . . >
c) Create a type Move representing a move in this game.
d) Write a function possible :: Game →
[Move] that produces a list of all possible moves for any
state.
e) Write a function move :: Game → Move →
Game that applies a valid move to a game state, producing a
new state.
f) Write an interactive program that allows a player at the terminal to play as the fox versus a computer player, who controls the hounds. For the computer player, use a dummy strategy that just chooses the first possible move. The player should enter their move as one of the string "ul", "ur", "dl" or "dr", where e.g. "ul" means to move up and left. If the game ends, print "You won!" or "You lost!" and exit.
For example:
> play H H H H . . . . . . . . . . . . . . . . . . . . . . . . F . . . Your move? ur . H H H H . . . . . . . . . . . . . . . . . . . F . . . . . . . Your move? ul . H H H . . . . H . . . . . . . . . . . F . . . . . . . . . . . Your move?
g) Modify the computer player to be stronger.
A mini-Sudoku puzzle looks like this:
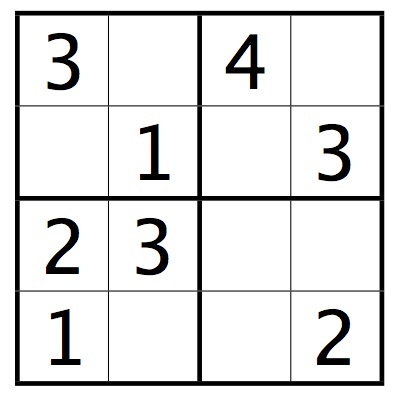
To solve the puzzle, you must place a number from 1 to 4 in every square so that the numbers in every row, column, and mini-square are distinct.
Write a program that reads a mini-Sudoku puzzle from standard input. Empty squares will be represented by the number 0:
3040 0103 2300 1002
The program should print out a solution to the puzzle if it can find one; otherwise it should print "no solution".
Write a program that reads a rectangular maze from standard input in the following format:
#####.### #...#...# #.#...#.# #.#####.# #.....#.# ###.#####
If there is any possible path from the top to the bottom, the program should print out the maze, highlighting some such path:
#####x### #xxx#x..# #x#xxx#.# #x#####.# #xxx..#.# ###x#####
If there is no such path, it should print "no path".
a) Write a function that takes a directed graph and returns True if the graph is cyclic, otherwise False.
b) Modify your function to work on an undirected graph.
In an undirected graph, a Hamiltonian cycle is a cycle that visits every vertex exactly once. A graph possessing a Hamiltonian cycle is said to be Hamiltonian.
Write a function that takes a graph in adjacency-list representation and returns a list containing the vertices in any Hamiltonian cycle in the graph, or Nothing if there is none.
Write a function that takes two graphs in adjacency list representation and returns true if the graphs are isomorphic.
Consider a simple language in which every program consists of a series of assignments, one per line. For example, here is a program:
x = 2x = 3 + xy = 10 + 2 * xa = (y - 15) * 20
In this language all values are integers, and constants are
non-negative integers. Integers have the same numeric range as an Int
in Haskell. Variable names consist of 1 or more lowercase letters.
Expressions may contain the operators '+',
'-', '*' and '/'. All
operators are left-associative. '*' and '/'
have higher precedence than '+' and '-'.
Any subexpression may be surrounded by parentheses. Every assignment
is of the form 'var = expression'. Whitespace may appear anywhere in
an input line.
Write a program that reads a program in this language and interprets it. The program should print out the final values of all variables in alphabetical order. For example:
a = 100 x = 5 y = 20