We have already studied how to analyze the running time of iterative functions, i.e. functions that use loops. We'd now like to do the same for recursive functions.
To analyze any recursive function's running time, we perform two steps. First, we write a recurrence, which is an equation that expresses the function's running time recursively, i.e. in terms of itself. Second, we solve the recurrence mathematically. In this class, we will generally derive solutions to recurrences somewhat informally. (In ADS 1 next semester, you will study this topic with more mathematical rigor.)
For example, consider this simple recursive function:
def fun1(n):
if n == 0:
return 0
return n * n + fun1(n - 1)The function computes the sum 12 + 22 + … + n2, using recursion to perform its task.
Let's write down a recurrence that expresses this
function's running time. Let T(N) be the time to run fun1(N).
The function performs a constant amount of work outside the recursive
call (since we assume that arithmetic operations run in constant
time). When it calls itself recursively, n decreases by 1. And so we
have the equations
T(0) = O(1)
T(N) = T(N - 1) + O(1)
Now we'd like to solve the recurrence. We can do so by expanding it algebraically. O(1) is some constant C. We have
T(N)
= C + T(N - 1)
= C + C + T(N – 2)
= …
= C + C +
... + C (N times)
=
N · C
= O(N)
The function runs in linear time. That's not a surprise, since an iterative loop to sum these numbers would also run in O(N).
When we write recurrences from now on, we will usually not bother to write a base case 'T(0) = O(1)', and will only write the recursive case, e.g. 'T(N) = T(N - 1) + O(1)'.
Now consider this function:
def fun2(n):
if n == 0:
return 0
s = 0
for i in range(n):
s += n * i
return s + fun2(n – 1)The 'for' loop will run in O(N), so the running time will follow this recurrence:
T(N) = T(N – 1) + O(N)
We can expand this algebraically. O(N) is CN for some constant C, so we have
T(N)
= CN + T(N – 1)
= CN + C(N – 1) + T(N – 2)
= CN + C(N
– 1) + C(N - 2) + T(N - 3)
= …
= C(N + (N – 1) + …
+ 1)
= C(O(N2))
= O(N2)
As another example, consider this recursive function that computes the binary representation of an integer:
def fun3(n):
if n == 0:
return ''
d = n % 2
return fun3(n // 2) + str(d)The work that the function does outside the recursive calls takes constant time, i.e. O(1). The function calls itself recursively at most once. When it calls itself, it passes the argument (n // 2). So we have
T(N) = T(N / 2) + O(1)
To solve this, let's again observe that O(1) is some constant C. We can write
T(N)
= C + T(N / 2)
= C + C + T(N / 4)
= …
= C + C + ...
+ C (log2(N)
times)
= C log2(N)
=
O(log N)
Next, consider this function:
def fun4(n):
if n == 0:
return 0
s = 0
for i in range(n):
s += i * i
return s + fun4(n // 2)The running time follows this recurrence:
T(N) = T(N / 2) + O(N)
Let O(N) = CN. Then we have
T(N)
= CN + T(N / 2)
= CN + C(N / 2) + T(N / 4)
= CN + C(N / 2)
+ C(N / 4) + T(N / 8)
…
= C(N + N / 2 + N / 4 + …)
=
C(2N)
= O(N)
These recurrences were relatively easy to solve, since they arose from recursive functions that call themselves at most once. When a recursive function calls itself twice or more, the resulting recurrence may not be quite so easy. For example, recall the Fibonacci sequence:
1, 1, 2, 3, 5, 8, 13, 21, ...
Its definition is
F1 = 1
F2 = 1
Fn = Fn - 1 + Fn - 2 (n ≥ 3)
We may directly translate this into a recursive Python function:
def fib(n):
if n <= 2:
return 1
return fib(n - 1) + fib(n - 2)Let T(N) be the running time of this function on an integer N ≥ 3. We have
T(N) = O(1) + T(N - 1) + T(N - 2)
Omitting the term O(1), we see that T(N) > T'(N), where
T'(N) = T'(N - 1) + T'(N - 2)
Now observe that this recurrence for T'(N) is just the same as for the Fibonacci numbers Fn themselves! This shows that T(N) is at least O(Fn).
Now, it can be shown that the Fibonacci numbers increase exponentially, and so T(N) also grows exponentially, i.e. faster than any polynomial function such as N2 or N4.
Why is this function so inefficient? The essential problem is that it will perform the same subcomputations over and over. For example, if we call fib(40), that will recursively call both fib(39) and fib(38). Those functions will make further recursive calls, and so on:
fib(40)
= fib(39) + fib(38)
= (fib(38) + fib(37)) + (fib(37) + fib(36))
= ...
The two instances of fib(37) above are separate repeated computations. As this tree expands, smaller subcomputations such as fib(20) and fib(10) will occur an enormous (exponential) number of times.
We could make this function much faster by caching the results of subcomputations so that each subcomputation occurs only once. We'll discuss this topic more in Programming 2 in next semester. For the moment, the important point is that recursion, though powerful, lets us easily write functions that will take exponential time to run.
As a step toward our next sorting algorithm, suppose that we have two arrays, each of which contains a sorted sequence of integers. For example:
a = [3, 5, 8, 10, 12] b = [6, 7, 11, 15, 18]
And suppose that we'd like to merge the numbers
in these arrays into a single array c
containing all of the numbers in sorted order.
A simple algorithm will
suffice. We can use integer variables i
and j
to point to members of a
and b,
respectively. Initially i
= j
= 0. At each step of the merge, we compare a[i]
and b[j].
If a[i] < b[j],
we copy a[i]
into the destination array, and increment i. Otherwise we copy b[j]
and increment j. The entire process will run in linear time, i.e. in
O(N) where N = len(a) + len(b).
Let's write a function to accomplish this task:
# Merge sorted arrays a and b into c, given that
# len(a) + len(b) = len(c).
def merge(a, b, c):
i = j = 0 # index into a, b
for k in range(len(c)):
if j == len(b): # no more elements available from b
c[k] = a[i] # so we take a[i]
i += 1
elif i == len(a): # no more elements available from a
c[k] = b[j] # so we take b[j]
j += 1
elif a[i] < b[j]:
c[k] = a[i] # take a[i]
i += 1
else:
c[k] = b[j] # take b[j]
j += 1We can use this function to merge the arrays a and b mentioned above:
>>> a = [3, 5, 8, 10, 12] >>> b = [6, 7, 11, 15, 18] >>> c = (len(a) + len(b)) * [0] >>> merge(a, b, c) >>> c [3, 5, 6, 7, 8, 10, 11, 12, 15, 18] >>>
We now have a function that merges two sorted arrays. We can use this as the basis for implementing a sorting algorithm called merge sort.
Merge sort has a recursive structure. To sort an array of n elements, it divides the array in two and recursively merge sorts each half. It then merges the two sorted subarrays into a single sorted array.
For example, consider merge sort’s operation on this array:
Merge sort splits the array into two halves:
It then sorts each half, recursively.
Finally, it merges these two sorted arrays back into a single sorted array:
Here's an implemention of merge sort, using our merge() function from the previous section:
def merge_sort(a):
if len(a) < 2:
return
mid = len(a) // 2
left = a[:mid] # copy of left half of array
right = a[mid:] # copy of right half
merge_sort(left)
merge_sort(right)
merge(left, right, a)Let's add merge sort to our performance graph, showing the time to sort random input data:
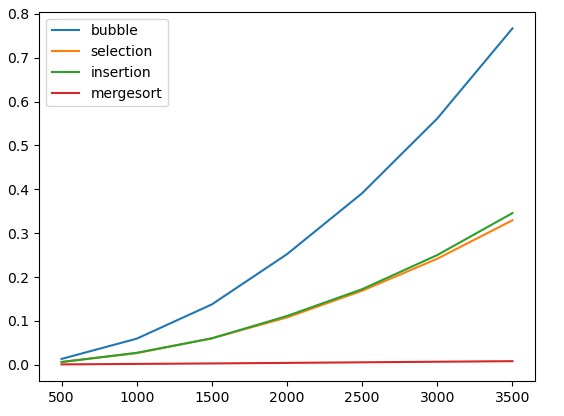
As we can see, merge sort is enormously faster than any of the other sorting methods that we have seen. Let's draw a plot showing the performance of only merge sort, with larger input sizes:
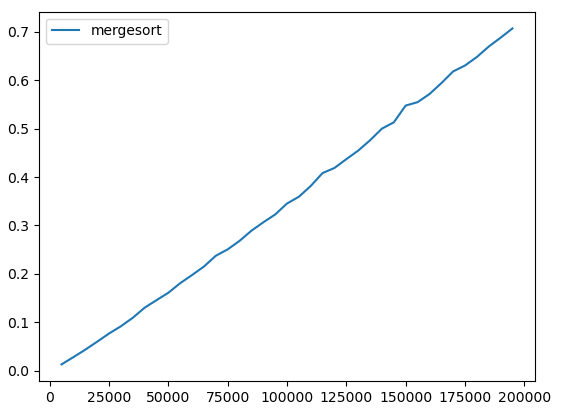
The performance looks nearly linear.
What is the actual big-O running time of merge
sort? In the code above, the helper function merge runs
in time O(N), where N is the length of the array c. The array slice
operations a[:mid] and a[mid:] also take
O(N). So if T(N) is the time to run merge_sort on an
array with N elements, then we have
T(N) = 2 T(N / 2) + O(N)
We have not seen this recurrence before. Let O(N) = CN for some constant C. We have T(N) = 2 T(N / 2) + CN, so we know that T(N) is the sum of all the terms here:
Let's expand each leaf using the same equation:
And again:
We can continue this process until we reach the base case T(1) = O(1). We'll end up with a tree with log2 N levels, since that's how many times we must divide by 2 to reach 1. Notice that the sum of the values on every level is CN: we have 2(C / 2) = 4 (C / 4) = N, for instance. So the total of all terms on all levels will be CN(log2 N). This informal argument has shown that
T(N) = O(N log N)
By the way, the tree above also illustrates the structure of the recursive calls that happen as the mergesort proceeds.
For large N, O(N log N) is much faster than O(N2), so mergesort will be far faster than insertion sort or bubble sort. For example, suppose that we want to sort 1,000,000,000 numbers. And suppose (somewhat optimistically) that we can perform 1,000,000,000 operations per second. An insertion sort might take roughly N2 = 1,000,000,000 * 1,000,000,000 operations, which will take 1,000,000,000 seconds, or about 32 years. A merge sort might take roughly N log N ≈ 30,000,000,000 operations, which will take 30 seconds. This is a dramatic difference!
We've
seen that merge sort is quite efficient. However, one potential
weakness of merge sort is that it will not run in
place:
it requires extra memory beyond that of the array that we wish to
sort. That's because the merge step won't run in place: it requires
us to merge two arrays into an array that is held in a different
region of memory. So any implementation of merge sort must make a
second copy of data at some point. (Ours does so in the lines 'left
= a[:mid]'
and 'right = a[mid:]',
since an array slice in Python creates a copy of a range of
elements.)
Quicksort is another sorting algorithm. It is efficient (typically significantly faster than mergesort) and is commonly used.
Quicksort sorts values in an array in place - unlike mergesort, which needs to use extra memory to perform merges. Given a range a[lo:hi] of values to sort in an array a, quicksort first arranges the elements in the range into two non-empty partitions a[lo:k] and a[k:hi] for some integer k. It does this in such a way that every element in the first partition (a[lo:k]) is less than or equal to every element in the second partition (a[k:hi]). After partitioning, quicksort recursively calls itself on each of the two partitions.
The high-level structure of quicksort is similar to mergesort: both algorithms divide the array in two and call themselves recursively on both halves. With quicksort, however, there is no more work to do after these recursive calls. Sorting both partitions completes the work of sorting the array that contains them. Another difference is that merge sort always divides the array into two equal-sized pieces, but in quicksort the two partitions are generally not the same size, and sometimes one may be much larger than the other.
Two different partitioning algorithms are in common use. In this course we will use Hoare partitioning, which works as follows. To partition a range of an array, we first choose some element in the range to use as the pivot. The pivot has some value p. Once the partition is complete, all elements in the first partition will have values less than or equal to p, and elements in the second partition will have values greater than or equal to p.
To partition the elements, we first define integer variables i and j representing array indexes. Initially i is positioned at the left end of the array and j is positioned at the right. We move i rightward, looking for a value that is greater than or equal to v (i.e. it can go into the second partition). And we move j leftward, looking for a value that is less than or equal to v. Once we have found these values, we swap a[i] and a[j]. After the swap, a[i] and a[j] now hold acceptable values for the left and right partitions, respectively. Now we continue the process, moving i to the right and j to the left. Eventually i and j meet. The point where they meet is the division point between the partitions, i.e. is the index k mentioned above.
Note that the pivot element itself may move to a different position during the partitioning process. There is nothing wrong with that. The pivot really just serves as an arbitrary value to use for separating the partitions.
For example, consider a partition operation on this array:
The array has n = 8 elements. Suppose that we choose 3 as our pivot. We begin by setting i = 0 and j = 7. a[0] = 6, which is greater than the pivot value 3. We move j leftward, looking for a value that is less than or equal to 3. We soon find a[6] = 2 ≤ 3. So we swap a[0] and a[6]:
Now a[1] = 5 ≥ 3. j moves leftward until j = 3, since a[3] = 3 ≤ 3. So we swap a[1] and a[3]:
Now i moves rightward until it hits a value that is greater than or equal to 3; the first such value is a[3] = 5. Similarly, j moves leftward until it hits a value that is less than or equal to 3; the first such value is a[2] = 1. So i = 3 and j = 2, and j < i. i and j have crossed, so the partitioning is complete. The first partition is a[0:3] and the second partition is a[3:8]. Every element in the first partition is less than every element in the second partition.
Notice that in this example the pivot element itself moved during the partitioning process. As mentioned above, this is common.
Here is an implementation of Hoare partitioning in Python:
from random import randrange
# We are given an unsorted range a[lo:hi] to be partitioned, with
# hi - lo >= 2 (i.e. at least 2 elements in the range).
#
# Choose a pivot value p, and rearrange the elements in the range into
# two partitions p[lo:k] (with values <= p) and p[k:hi] (with values >= p).
# Both partitions must be non-empty.
#
# Return k, the index of the first element in the second partition.
def partition(a, lo, hi):
# Choose a random element as the pivot, avoiding the first element
# (see the discussion below).
p = a[randrange(lo + 1, hi)]
i = lo
j = hi - 1
while True:
# Look for two elements to swap.
while a[i] < p:
i += 1
while a[j] > p:
j -= 1
if j <= i: # nothing to swap
return i
a[i], a[j] = a[j], a[i]
i += 1
j -= 1At all times as the code above runs,
for all x < i, a[x] ≤ p
for all x > j, a[x] ≥ p
The code that decides when to exit the loop and computes the return value is slightly tricky. Let's distinguish two cases that are possible when we hit the test 'if j <= i':
Suppose that i and j have crossed, i.e. j + 1 = i. Then
For all x ≤ j we have x < i, so a[x] ≤ p.
Similarly, for all x ≥ i we have x > j, so a[x] ≥ p.
Thus j is the last element of the first partition, and i is the first element of the second partition. We return i (which is the same as j + 1).
Now suppose that i and j have met but have not crossed, i.e. i = j. Then it must be that a[i] = a[j] = p (the pivot value). For if that array element held any other value, then in the preceding 'while' loops either i would have continued incrementing, or j would have continued decrementing.
So now the situation looks as follows:
For all x < i = j, we know that a[x] ≤ p.
a[i] = a[j] = p.
For all x > i = j, we have a[x] ≥ p.
At this point it may seem that we can return either i or i + 1. To keep our code simple, we'd like to return i, just as in the previous case. However, we must be a bit careful. Suppose that the first element of the array is the pivot, and i and j meet at that element, i.e. i = j = 0. In this situation if we returned i (i.e. 0), then the left partition would be empty. That's unacceptable: it would cause quicksort to recursive infinitely, since it would recursively sort the right partition which would be just the same as before. For this reason, we must avoid the first array element when we choose a random pivot at the beginning of the function above. That guarantees that if i and j meet, it will not be at index 0. (Similarly, if we returned i + 1 here we'd need to avoid the last array element when choosing a pivot).
In summary, in either of these cases i is a correct value to return.
With partition
in place, we can easily write our top-level quicksort
function:
# Sort a[lo:hi].
def qsort(a, lo, hi):
if hi - lo <= 1:
return
k = partition(a, lo, hi)
qsort(a, lo, k)
qsort(a, k, hi)
def quicksort(a):
qsort(a, 0, len(a)) To analyze the performance of quicksort, first
consider the running time of the helper function partition(a,
lo,
hi)
as a function of N =
hi -
lo. The first inner while loop has body "i += 1".
Certainly this statement can run at most N times, because i will
always remain within the range lo .. hi. So the total running time of
this inner while loop is O(N). Similarly, the total running time of
the second inner while loop with body "j -= 1" is also
O(N). The outer 'while True' loop iterates at most N times, and its
body (excepting the inner loops, which we have already considered)
runs in O(1) on each iteration. And so the total running time of
partition() is O(N).
Now let's consider the running time of the recursive function qsort(a, lo, hi) as a function of N = hi - lo. In the best case, quicksort divides the input array into two equal-sized partitions at each step. Then we have
T(N) = 2 T(N / 2) + O(N)
This is the same recurrence we saw when we analyzed merge sort previously! As we know, its solution is
T(N) = O(N log N)
In the worst case, at each step one partition has a single element and the other partition has all remaining elements. Then
T(N) = T(N – 1) + O(N)
This yields
T(N) = O(N2)
Now suppose that instead of choosing random pivot elements, we always chose the second element as a pivot (since we must avoid the first):
p = a[1]
And suppose that the input array is already sorted (which is certainly possible in many real-world situations). Then in each partition operation, the left partition would contain only a single element, and the right partition would contain all the remaining elements. This would cause this worst-case behavior, and the sort would run in O(N2). Similarly, if we always chose the last element as a pivot, we would also get worst-case behavior if the input array is already sorted.
For this reason, it is better to choose a random pivot as we did in our implementation above.
With pivot elements chosen at random, the worst-case running time of Quicksort is still O(N2), however the expected running time is O(N log N), and the chance of quadratic behavior is astronomically small. (You may see a proof of this in ADS 1 next semester.)
Here's one more small point. In the partition function, when we increment i and decrement j we stop when we see a value that is equal to the pivot. We will then swap that value into the other partition. Is this necessary? Could we simply skip over values that are equal to the pivot?
Suppose that we modified the code to look like this:
while a[i] <= p:
i += 1
while a[j] >= p:
j -= 1And suppose that we are sorting a range of values a[lo:hi] that are all the same, e.g. [4, 4, 4, 4]. The pivot will be 4. Now we will increment i until it runs past the end of the array on the right side, which is an error. For this reason, we must use strict equality (<, >) in these 'while' conditions.