A delegate is a value that represents a function or method. It's similar to to a function object in Python, or a function pointer in languages such as C.
The delegate keyword declares a new
delegate type. For example:
delegate bool IntCondition(int i);
With this declaration, an IntCondition is a type of delegate that takes an integer argument and returns a boolean.
We can now declare a variable of type IntCondition, and use it to refer to a function or method of corresponding type:
bool isOdd(int i) => i % 2 == 1; IntCondition c = isOdd; …
We can invoke the delegate using function call syntax:
WriteLine(c(4)); // writes False
In the example above, the delegate c refers to a static method odd(). A delegate may also refer to an instance method, in which case it actually references a particular object on which the method will be invoked. For example:
class Interval {
public int low, high;
public Interval(int low, int high) { this.low = low; this.high = high; }
public bool contains(int i) {
return low <= i && i <= high;
}
}
IntCondition c = new Interval(1, 5).contains;
IntCondition d = new Interval(3, 7).contains;
WriteLine(c(2)); // writes True
WriteLine(d(2)); // writes FalseHere is a function that counts how many elements in an array of integers satisfy an arbitrary condition:
int count(int[] a, IntCondition c) {
int n = 0;
foreach (int i in a)
if (c(i))
++n;
return n;
}We can invoke this function as follows:
bool isEven(int i) => i % 2 == 0;
int[] a = { 3, 4, 5, 6, 7 };
WriteLine(count(a, isEven)); // writes 2Delegates may be generic:
delegate bool Condition<T>(T t); // maps type T to bool
Here is the count() function from above, rewritten to work on an array of any type T. Notice that the function itself must also be generic (indicated by the "<T>" after the method name).
int count<T>(T[] a, Condition<T> c) {
int n = 0;
foreach (T x in a)
if (c(x))
++n;
return n;
}The standard library contains several useful generic delegate types. The built-in type Predicate<T> is exactly equivalent to the type Condition<T> that we just defined:
delegate bool Predicate<T>(T obj);
Additionally, the built-in type Func<T, U> represents an arbitrary function from type T to type U:
delegate U Func<T, U>(T arg);
A lambda expression is an anonymous function that can appear inside another expression. (It's similar to an lambda expression in Python, which we saw last semester).
For example, here's a generic function map() that applies a Func<T, U> to every element of an array of type T[], returning a new array of type U[]:
U[] map<T, U>(T[] a, Func<T, U> f) {
U[] b = new U[a.Length];
for (int i = 0; i < a.Length ; ++i)
b[i] = f(a[i]);
return b;
}We can define a function and pass it to map():
int plus2(int i) => i + 2;
int[] a = { 100, 200, 300 };
int[] b = map(a, plus2);Alternatively, we can invoke map() using a lambda expression:
int[] b = map(a, i => i + 2);
Here, i => i + 2 is a lambda expression. It's an
anonymous function that takes an integer parameter i and returns the
value i + 2.
A lambda expression may refer to parameters or local variables in its containing function or method. For example, suppose we want to write a method that adds a given value k to each element in an array. We could write a local method and pass it to map():
int[] add_k(int[] a, int k) {
int f(int i) {
return i + k;
}
return map(a, f);
}Or we can use a lambda expression that adds k directly:
int[] add_k(int[] a, int k) {
return map(a, i => i + k);
}The System.Linq namespace contains many methods that operate on sequences, i.e. objects that implement IEnumerable<T>. These are extension methods, meaning that they are implemented in the System.Linq namespace rather than in IEnumerable<T> itself. However for the purpose of calling these methods that makes no difference, and you can invoke them directly on any enumerable object.
Useful methods include Select(), which maps a function over a sequence, and Where(), which filters a sequence, keeping only the elements for which a given condition is true. Most of these methods return a new sequence, i.e. another IEnumerable<T>. You can call the ToArray() or ToList() methods to gather a sequence's elements into an array or list.
For example, suppose that we want to keep only the odd values in an array, and add 10 to every remaining value. We might write
int[] a = { 15, 16, 17, 18, 19 };
int[] b = a.Where(i => i % 2 == 1).Select(i => i + 10).ToArray();There are many other useful methods such as Concat(), OrderBy(), and Reverse(). You can read about these in our quick reference documentation.
Note that the System.Linq namespace is imported automatically by C#'s implicit usings feature. As we've seen before, this feature is not enabled on ReCodEx, so you'll need to import System.Linq explicitly there.
C# includes special syntax for calling some of the Linq methods. For example, instead of
int[] b = a.Where(i => i > 10).Select(i => i + 10).ToArray();
we can write
int[] b = (from i in a where i > 10 select i + 10).ToArray();
This is the closest approximation in C# to a list comprehension in Python, where we could write
# Python code
b = [i + 10 for i in a if i > 10]
As usual, the C# equivalent is more verbose.
We can use recursion to solve many problems of a combinatorial nature, such as generating subsets, combinations, or permutations of a set. As we solve these problems we can use recursion to explore a tree of possibilities.
As a first example, suppose that we'd like to
write a function that
takes an integer n and
prints out all possible strings of length n containing only
characters from the set {'a', 'b', 'c'}.
For example, if n = 2 then we
will print these strings:
aa ab ac ba bb bc ca cb cc
And if n = 3:
aaa aab aac aba abb abc aca acb acc baa bab bac …
There will be 3n strings in the output list. That's because there are 3 possible choices for the first letter, 3 for the second letter, and so on for each of the n letters.
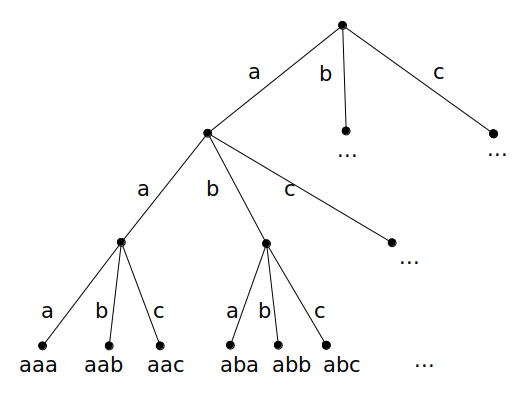
We can imagine a series of choices that we must make as we choose a string to print out. We can draw these in a tree. For example, if n = 3:

At each step, we choose the letter 'a', 'b' or 'c'. Affter we have made N choices, we have a string that we can print.
Any algorithm that can generate these strings for any given N will surely take exponential time, since the length of the output is exponential in N. This is a sign that we will probably need to use recursion to solve this problem, since a set of loops without recursion will generally run in polynomial, not exponential, time.
We will study several different solutions to this problem. Each of them will use a different technique that we may apply to other problems as well.
We can recursively explore this tree of choices. As the recursion descends, we will accumulate all choices we've made so far and pass them as a prefix string to the next level of the recursion. When we have made N choices, we have reached a leaf of the tree and will print out the string we have built.
Here is our solution:
// recursive helper function
void abc_r(string prefix, int n) {
if (n == 0)
WriteLine(prefix);
else
foreach (char c in "abc")
abc_r(prefix + c, n - 1);
}
void abc(int n) => abc_r("", n);In this solution the parameter n represents the number of choices that remain to be made, i.e. the number of string characters that we still must generate. At each step there are 3 possible choices, so the function abc_r() calls itself 3 times.
As another possibility, as the recursion descends we can push all choices we've made so far onto a stack. Once we have made N choices, we can print out the values on the stack. Each time the recursion returns, we pop our last choice off the stack, restoring its previous state. This solution might look like this:
void abc2(int n) {
Stack<char> stack = new Stack<char>();
void go(int n) {
if (n == 0)
WriteLine(string.Join("", stack.Reverse()));
else {
foreach (char c in "abc") {
stack.Push(c);
go(n - 1);
stack.Pop();
}
}
}
go(n);
}We call the Linq method Reverse() above so that we print out characters in the order we chose them. For example, if we choose 'b', then 'a', then 'c', then iterating over the stack will produce the values 'c', 'a', and 'b' in that order. Reversing produces the order 'b', 'a', 'c'.
In solution 1 above, we never have to undo a choice that we have made, because the expression 'prefix + c' creates a copy of the prefix string with the additional character c. The original prefix string remains unchanged (as it must be, since strings are immutable in C#). However, this stack-based solution may be slightly more efficient because it never copies the set of choices accumulated so far.
When we study larger problems that explore an exponential state space, we will often see this same choice: we may either (a) copy the state each time we recurse, or (b) modify the state before recursing, then undo the change afterwards.
In the stack-based solution above, the stack's depth will always be exactly n whenever we reach the base case and print out a solution. And so in fact we can use a fixed-size array in place of a stack, which will simplify our code a bit. Our solution will look like this:
void abc3(int n) {
char[] a = new char[n];
void go(int i) {
if (i == n)
WriteLine(string.Join("", a));
else
foreach (char c in "abc") {
a[i] = c;
go(i + 1);
}
}
go(0);
}This is a nice simplification. However, in some recursive problems the number of elements in a solution may vary, and then a stack-based solution may be more appropriate.
We can actually solve this problem non-recursively, by extracting digits from an integer. To see how this will be possible, suppose that instead of the characters 'a', 'b' and 'c' we want to generate the digits 0, 1, and 2. Then our output for N = 3 will look like this:
000 001 002 010 011 012 020 021 022 100 101 …
This is simply all 3-digit numbers in base 3!
For a given N, there are 3N N-digit numbers in base 3, which is exactly the number of possible solutions that we saw before. So we may simply loop through integers from 0 to 3N – 1, extract a series of base-3 digits from each, and convert each such digit to a character 'a', 'b' or 'c'. Here is a possible solution:
void abc3(int n) {
string convert(int i) {
string s = "";
for (int k = 0 ; k < n ; ++k) {
s = "abc"[i % 3] + s;
i = i / 3;
}
return s;
}
int p = (int) Math.Pow(3, n);
for (int i = 0 ; i < p ; ++i)
WriteLine(convert(i));
}Another typical combinatorial problem is generating all subsets of a set. Specifically, suppose that for any N we'd like to generate all subsets of the set {1, 2, …, N}. For N = 3, our output might look like this (in some order):
{ }
{ 1 }
{ 2 }
{ 1 2 }
{ 3 }
{ 1 3 }
{ 2 3 }
{ 1 2 3 }One way to view this problem is as a series of N choices, one for each of the values {1, 2, …, N}. In each choice, we decide whether a certain value will be absent from the set or present in it. Each of these N choices is a binary decision, and so there will be 2N possible solutions.
We can solve this problem using any of the techniques that we saw above for the abc problem. Let's write a solution using a prefix parameter:
// recursive helper function
void subsets_r(string prefix, int i, int n) {
if (i > n)
WriteLine("{" + prefix + "}");
else {
subsets_r(prefix + i + " ", i + 1, n); // i is in the subset
subsets_r(prefix, i + 1, n); // i is not in the subset
}
}
void subsets(int n) => subsets_r(" ", 1, n);Our decisions are binary, so our recursive function calls itself twice, once for each possible choice.
Let's run it:
subsets(4);
This will produce this output:
{ 1 2 3 4 }
{ 1 2 3 }
{ 1 2 4 }
{ 1 2 }
{ 1 3 4 }
{ 1 3 }
{ 1 4 }
{ 1 }
{ 2 3 4 }
{ 2 3 }
{ 2 4 }
{ 2 }
{ 3 4 }
{ 3 }
{ 4 }
{ }