Write a generic method
T[] filter<T>(T[] a, Predicate<T> p)
that selects only the elements of a for
which the given predicate is true.
Write a generic method max_by() that takes an array plus a function f. The method should return the array element x for which f(x) is the greatest, or null if the array is empty. For example:
string[] a = { "red", "yellow", "blue", "green" };
WriteLine(max_by(a, s => s.Length)); // writes "yellow"The method should work for any array type and for any function that maps the array type to a comparable type.
Write a generic function
void sort<T>(T[] a, Comparison<T> f)
that can sort an array using an arbitrary function to compare elements. The delegate type Comparison<T> is defined in the standard library as follows:
delegate int Comparison<T>(T x, T y);
Given two objects x and y of type T, a Comparison<T> returns
You may use any sorting algorithm that you like.
Solve Project Euler Problem 1 in a single line of code using Linq methods or Linq syntax:
Find the sum of all the multiples of 3 or 5 below 1000.
In the lecture we wrote a function that prints all subsets of {1, ..., N} using a prefix parameter. Rewrite this function using any of the other 3 techniques that we used for solving the abc problem.
Write a function void
permutations(string s) that prints all permutations of a
string. For example, permutations("cat")
might print
cat cta act atc tca tac
Write a function void
combinations(int[] a, int k) that takes an array a and an
integer k, and prints
all combinations of k elements of a. For example, the call
int[] a = { 2, 4, 6, 8, 10};
combinations(a, 3);might produce this output:
2 4 6 2 4 8 2 4 10 2 6 8 2 6 10 2 8 10 4 6 8 4 6 10 4 8 10 6 8 10
A student is walking up a staircase that contains N stairs. On each step, the student may walk up either 1, 2, or 3 stairs. Write a program that reads N and prints out all possible ways that exist to climb the stairs in this fashion. For example, if N = 4 then the program might print (in some order)
1 + 1 + 1 + 1
1 + 1 + 2
1 + 2 + 1
1 + 3
2 + 1 + 1
2 + 2 3 + 1
A composition of a non-negative integer n is a sequence of positive integers that add up to n. Order matters: 1 + 3 and 3 + 1 are different compositions of 4.
a) Write a function compositions(n) that prints
all compositions of an integer n. For example, compositions(3)
will print (in some order):
1 + 1 + 1 1 + 2 2 + 1 3
b) Find an algebraic formula that expresses how many compositions of any integer N exist, as a function of N.
A partition of a non-negative integer n is a sequence of positive integers that add up to n. Order does not matter: 1 + 3 and 3 + 1 are the same partition of 4.
Write a function partitions(n) that prints all
compositions of an integer n. For example, compositions(3)
will print (in some order):
1 + 1 + 1 2 + 1 3
Write a function change(n) that takes a positive integer n representing a number of Czech crowns. The function should print out all possible ways to form the sum, using Czech coins worth 1 Kč, 2 Kč, 5 Kč, 10 Kč, 20 Kč, or 50 Kč. For example, change(8) will print (in some order):
5 + 2 + 1 5 + 1 + 1 + 1 2 + 2 + 2 + 2 2 + 2 + 2 + 1 + 1 2 + 2 + 1 + 1 + 1 + 1 2 + 1 + 1 + 1 + 1 + 1 + 1 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
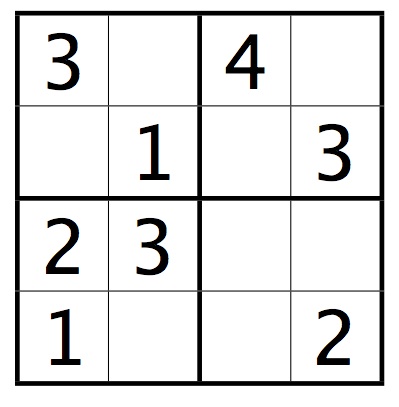
A mini-Sudoku puzzle looks like this:

To solve the puzzle, you must place a number from 1 to 4 in every square so that the numbers in every row, column, and mini-square are distinct.
Write a method that reads a mini-Sudoku puzzle from standard input. Empty squares will be represented by the number 0:
3040 0103 2300 1002
The method should print out a solution to the puzzle if it can find one, otherwise null.
Write a function that takes an undirected graph G in adjacency-list representation. The function should determine whether it is possible to color the graph with three colors (red, green, blue) such that no two adjacent vertices have a same color. If it is, it should print out a valid coloring.
A
clique
of a graph is a subgraph that is connected, i.e. in which there are
edges between all pairs of vertices. Write a function clique
that takes an undirected graph in adjacency-matrix representation and
an integer N, and returns true if the graph has any clique of size N.
(No efficient algorithm is known to solve this problem, so you will
need to enumerate all possible cliques.)