Last week we talked about arithmetic expressions in infix, prefix, and postfix notation. We will now discuss how to store and work with arithmetic expressions in a program.
We may store expressions using an expression tree, which is a form of abstract syntax tree. An expression tree reflects an expression’s hierarchical structure. For example, here is an expression tree for the infix expression ((3 + 4) * (2 + 5)):
Note that this expression tree also corresponds to the prefix expression * + 3 4 + 2 5, or the postfix expression 3 4 + 2 5 + *. Equivalent expressions in infix, prefix or postfix form will always have the same tree! That’s because this tree reflects the abstract syntax of the expression, which is independent of concrete syntax which defines how expressions are written as strings of symbols.
We can store expression trees using
objects in Python.
We'll have a parent class Expr representing any expression, with two
subclasses for our different node types. Every leaf node holds an
integer constant, and will be represented by a node of class IntExpr.
Every interior node of the tree represents
a binary operation, and will be represented by a node of class
OpExpr. Here are definitions for these classes:
class Expr:
pass
class IntExpr(Expr):
def __init__(self, val):
self.val = val
class OpExpr(Expr):
def __init__(self, op, left, right):
self.op = op
self.left, self.right = left, rightWe can build the expression tree in the picture above as follows:
left = OpExpr('+', IntExpr(3), IntExpr(4))
right = OpExpr('+', IntExpr(2), IntExpr(5))
tree = OpExpr('*', left, right)If we have an expression tree in memory, we may wish to evaluate it, which means to compute its value. For example, when we evaluate the expression (4 + 5) * (2 + 1), we get the value 27.
Let's write a method eval() for evaluating an expression, with implementations in the IntExpr and OpExpr classes:
# in class IntExpr
def eval(self):
return self.val
# in class OpExpr
def eval(self):
l = self.left.eval()
r = self.right.eval()
match self.op:
case '+': return l + r
case '-': return l - r
case '*': return l * r
case '/': return l // r
case '_': assert FalseLet's try it out on the small expression tree that we built above representing the expression ((3 + 4) * (2 + 5)):
>>> tree.eval() 49 >>>
Given an expression tree, it’s not hard to convert it to a string representation. For example, we can generate an expression in prefix notation as follows:
# in class IntExpr
def to_prefix(self):
return str(self.val)
# in class OpExpr
def to_prefix(self):
return f'{self.op} {self.left.to_prefix()} {self.right.to_prefix()}'Let's try it on our small expression tree:
>>> tree.to_prefix() '* + 3 4 + 2 5'
Generating an expression in postfix notation will be similar.
Now let's consider generating an infix expression. We've decided that we will have no operator precedence, so we will generate a fully parenthesized expression that so that our expression will be unambiguous. Here is the code:
# in class IntExpr
def to_infix(self):
return str(self.val)
# in class OpExpr
def to_infix(self):
return f'({self.left.to_infix()} {self.op} {self.right.to_infix()})'Let's try it:
>>> tree.to_infix() '((3 + 4) * (2 + 5))'
We have seen how to convert an expression tree to a string in infix, prefix, or postfix notation.
Now let's consider the inverse problem: given a string in infix, prefix, or postfix notation we would like to parse it into an expression tree.
Many parsers are divided into two phases. In the first phase, called lexical analysis, we break the input string into a series of tokens. In the second phase we examine the tokens and use them to construct an expression tree.
We will follow this approach. For our simple
expression language, a token will be either an integer constant
(represented by a Python int) or one of the symbols '(', ')', '+',
'-', '*' or '/' (represented by a Python string). For example, the
string '(4 + 15) * (22 - 1)' has these tokens:
( 4 + 15 ) * ( 22 - 1 )
Let's write a class that performs lexical analysis for this simple language.
class Lexer:
def __init__(self, s):
self.s = s
self.i = 0 # position of next token
# Read and return the next token (an int or a char),
# or return None if there are no more.
def next(self):
# move past spaces
while self.i < len(self.s) and self.s[self.i] == ' ':
self.i += 1
if self.i >= len(self.s):
return None
c = self.s[self.i]
self.i += 1
if c.isdigit(): # start of an integer constant
t = c
while self.i < len(self.s) and self.s[self.i].isdigit():
t += self.s[self.i]
self.i += 1
return int(t)
assert c in '+-*/()', 'invalid character'
return cLet's try it:
>>> l = Lexer('(4 + 15) * (22 - 1)')
>>> l.next()
'('
>>> l.next()
4
>>> l.next()
'+'
>>> l.next()
15
>>> l.next()
')'
>>> l.next()
'*'The set of all valid expressions in infix (or prefix, or postfix) syntax forms a language. When we write a parser for any language, it's helpful to have a grammar, which is a formal definition of the language's syntax.
As a
first step, consider the language of arithmetic expressions in
prefix form, with non-negative integer constants and the binary
operators +, -, *, and /.
We can formally define the syntax of this language using the
following context-free grammar:
digit = '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9' int = digit | int digit op = '+' | '-' | '*' | '/' expr = int | op expr expr
Context-free grammars are commonly used to define programming languages. A grammar contains non-terminal symbols (such as digit, op, expr) and terminal symbols (such as '0', '1', '2', …, '+', '-', '*', '/'), which are characters. A grammar consists of a set of production rules that define how each non-terminal symbol can be constructed from other symbols. These rules collectively define which strings of terminal symbols are syntactically valid. (You will study context-free grammars in more detail in more advanced courses, such as an automata course.)
The first production rule above says that a digit
is any of the characters '0', '1', ..., '9'. The second rule
"int = digit | int digit" says that
an integer is either a digit, or an integer followed by a digit. To
put it differently, this is a recursive rule stating that an integer
consists of any number of digits. We have already written a simple
lexical analyzer that embodies these first two rules.
The third rule above defines the set of valid operator characters. The fourth rule is recursive, and is the most important: it says that every expression is either an integer constant, or an operator followed by two expressions.
Following the grammar above, we would now like to write a function that can parse arithmetic expressions in prefix notation. We'll use the lexical analyzer we wrote above to generate tokens. We will write a nested recursive function parse() that reads a subexpression at the current token position and returns an expression tree for it. Here is the code:
# Given a string containing an expression in prefix syntax,
# parse it into an expression tree.
def parse_prefix(s):
r = Lexer(s)
# Parse a subexpression starting at the current point.
def parse():
t = r.next() # token
if isinstance(t, int):
return IntExpr(t)
assert t in '+-*/', 'invalid operator'
left = parse()
right = parse()
return OpExpr(t, left, right)
return parse()Notice that the structure of the recursive function parse() follows the grammar rule for prefix expressions:
expr = digit | op expr expr
To put it differently, we have written a recursive-descent parser for this grammar. In fact many compilers for real-world programming languages also use recursive-descent parsers (though this is not the only possible way to write a parser).
Let's parse a prefix expression, then use the resulting expression tree to convert back into prefix notation, and also into infix notation:
>>> e = parse_prefix('* + 3 4 - 5 2')
>>> e.to_prefix()
'* + 3 4 - 5 2'
>>> e.to_infix()
'((3 + 4) * (5 - 2))'
>>> Parsing an infix expression is not much more difficult. Let's modify the context-free grammar that we wrote above so that it will represent infix expressions. We only need to change the last line:
digit = '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
int = digit | int digit
op = '+' | '-' | '*' | '/'
expr = int | '(' expr op expr ')'Notice that in this grammar, all expressions must be fully parenthesized. That is to say, whenever we apply an operator to two operands, we must place parentheses around the result. This ensures that our grammar is unambiguous.
We may now write a recursive function that mirrors the rule for expressions, i.e. the last line in the grammar above:
# Given a string containing an expression in infix syntax,
# parse it into an expression tree.
def parse_infix(s):
r = Lexer(s)
# Parse a subexpression starting at the current point.
def parse():
t = r.next()
if isinstance(t, int):
return IntExpr(t)
assert t == '(', 'expected ('
left = parse()
op = r.next()
assert op in '+-*/', 'invalid operator'
right = parse()
assert r.next() == ')', 'expected )'
return OpExpr(op, left, right)
return parse()Once we have parsed an infix expression, we can easily evaluate it, or convert to a prefix representation:
>>> e = parse_infix('((2 + 3) * (4 + 5))')
>>> e.eval()
45
>>> e.to_prefix()
'* + 2 3 + 4 5'In this lecture we did not have time to discuss how to parse an expression in postfix form. Briefly, a recursive-descent parser will not work for this sort of expression; instead, we need to use a stack. Each time the parser sees an integer constant, it will push an IntExpr node to the stack. When it sees an operator character, it will pop two expressions from the stack and push an OpExpr node that combines them. When it has read the entire input string, the stack will contain a single element, namely the root node of an expression tree for the entire input expression. You may wish to think about this more and attempt to implement a postfix expression parser as an exercise.
In the last lecture we learned about the breadth-first search algorithm, and learned that we can use it to search in a state space. As an extended example, let's use a breadth-first search to solve the 8-puzzle, a classic puzzle that looks like this:
The 8-puzzle contains 8 sliding tiles within a 3 x 3 grid. At each step, you may slide a tile into the empty space. The goal is to reach the goal state containing the numbers 1 through 8 in order, with the empty space at the lower right:
How many states does the 8-puzzle have? To construct any state, we may first choose any of 9 possible positions for tile number 1. Then we have 8 choices for tile 2, and so on. So this shows that there may be as many as 9! = 362,880 states. However, it is not immediately obvious whether all these states are reachable from the goal state.
We may imagine that the states form a graph with 362,880 vertices. In this graph, each state's neighbors are the states that you can reach by performing any action in that state. All actions in this puzzle are reversible, so the graph is undirected.
In any state in which the blank tile is in a corner, there are only 2 possible actions. If the blank tile is along an edge, there are 3 possible actions, and if it's in the center then there are 4 possible actions. So every vertex of this graph has degree 2, 3, or 4. In 4/9 of all states the blank is in a corner, in 4/9 of states it's on an edge and in only 1/9 of states is it in the center. So the average degree of the graph is (4 ⋅ 2 + 4 ⋅ 3 + 1 ⋅ 4) / 9 = 2.67. We see that this graph is fairly sparse.
Let's perform a breadth-first search of this graph, starting from the goal state. That will discover all states that are reachable from the goal state. It will also find the shortest distance from the goal state to every other reachable state. As we search, we'll count how many states there are at each distance.
We'll store each puzzle state as a 2-dimensional
array in Python, i.e. a list of lists. Each element will be an
integer from 1 to 8, or 0 to represent the empty space. For example,
the goal state is [[1, 2, 3], [4, 5, 6], [7, 8, 0]].
We must first write a function that will find all neighbors of a given state:
def find_zero(p):
for x in range(3):
for y in range(3):
if p[x][y] == 0:
return x, y
assert False
dirs = [(1, 0), (-1, 0), (0, 1), (0, -1)]
# Given a puzzle state p, return a list of its neighbors.
def neighbors(p):
n = []
zx, zy = find_zero(p)
for dx, dy in dirs:
x1, y1 = zx + dx, zy + dy
if 0 <= x1 < 3 and 0 <= y1 < 3:
p1 = [row.copy() for row in p] # copy the state
p1[zx][zy] = p1[x1][y1]
p1[x1][y1] = 0
n.append(p1)
return nNow we may write our breadth-first search. We'll need a visited set to keep track of all states we've already seen. One slight complication is that we may not store a list in a Python set:
>>> s = set() >>> s.add([[1, 2, 3], [4, 5, 6], [7, 8, 0]]) Traceback (most recent call last): File "<stdin>", line 1, in <module> TypeError: unhashable type: 'list'
As a workaround, let's write a function that can convert a list of lists to a tuple of tuples:
def to_tuple(p):
return tuple(map(tuple, p))
>>> to_tuple([[1, 2, 3], [4, 5, 6], [7, 8, 0]])
((1, 2, 3), (4, 5, 6), (7, 8, 0))Here is our breadth-first search code:
from collections import defaultdict, deque
import matplotlib.pyplot as plt
def bfs(start):
visited = { to_tuple(start) }
q = deque()
q.append((start, 0))
total = 0 # total number of discovered states
count = defaultdict(int) # number of states at each distance
dist = 0
while len(q) > 0:
s, dist = q.popleft()
total += 1
count[dist] += 1
for n in neighbors(s):
nt = to_tuple(n)
if nt not in visited:
visited.add(nt)
q.append((n, dist + 1))
print(f'{total} states are reachable')
print(f'largest distance = {dist}')
plt.bar(list(count.keys()), list(count.values()))
plt.xlabel('distance from goal')
plt.ylabel('number of states')
plt.show()Let's run the search, starting from the goal state:
>>> bfs([[1, 2, 3], [4, 5, 6], [7, 8, 0]]) 181440 states are reachable largest distance = 31
We see that only half of the 362,880 possible states are reachable from the goal state. And so the state graph is not connected. It actually contains two connected components, each of which contains half of the states.
The function above displays this plot:
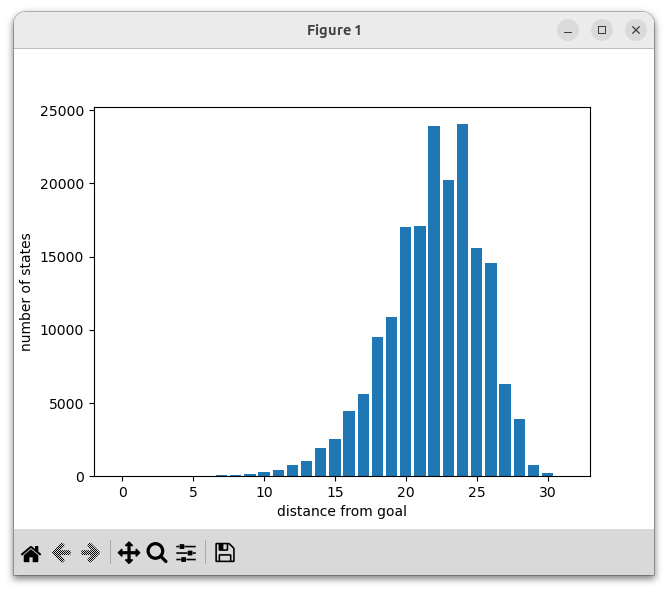
We see that a large number of states are at a distance of 20 to 25 moves from the goal. The output above showed that the largest distance from the goal is 31, so any puzzle position can be solved in at most 31 moves.
Finally, here is a graphical program written using Tkinter that displays the 8-puzzle. In this program, click any tile to slide it into the empty space. Press the 'r' key to shuffle the puzzle into a random solvable state. When you press the 's' key, the program will use our breadth-first search code to find a solution to the puzzle, and will move the blocks through the steps of the solution.