We can use recursion to solve many problems of a combinatorial nature, such as generating subsets, combinations, or permutations of a set. In these problems, we use recursion to explore an exponential tree of possibilities.
As a first example, let's suppose that we'd like
write a function that
takes an integer n and
prints out all possible strings of length n containing only
characters from the set {'a', 'b',
'c'}. For example, if n = 2
then we will print these
strings:
aa ab ac ba bb bc ca cb cc
And if n = 3:
aaa aab aac aba abb abc aca acb acc baa bab bac …
There will be 3n strings in the output list. That's because there are 3 possible choices for the first letter, 3 for the second letter, and so on for each of the n letters.
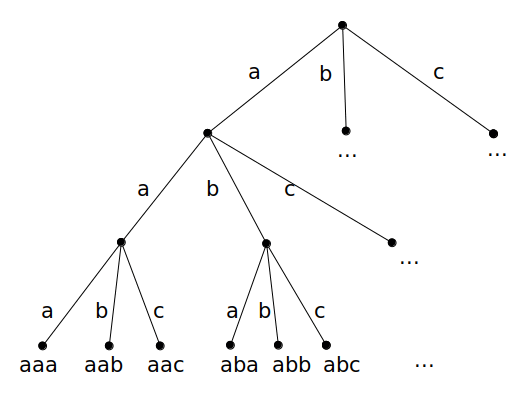
We can imagine a series of choices that we must make as we choose a string to print out. We can draw these in a tree. For example, if n = 3:

At each step, we choose the letter 'a', 'b' or 'c'. Affter we have made N choices, we have a string that we can print.
Any algorithm that can generate these strings for any given N will surely take exponential time, since the length of the output is exponential in N. This is a sign that we will probably need to use recursion to solve this problem, since a set of loops without recursion will generally run in polynomial, not exponential, time.
We will study 4 different solutions to this problem. Each of them will use a different technique that we may apply to other problems as well.
We can recursively explore this tree of choices. As the recursion descends, we will accumulate all choices we've made so far and pass them as a prefix parameter to the next level of the recursion. When we have made N choices, we have reached a leaf of the tree and will print out the string we have built.
Here is our solution:
// recursive helper function
void abc_r(string prefix, int n) {
if (n == 0)
WriteLine(prefix);
else
foreach (char c in "abc")
abc_r(prefix + c, n - 1);
}
void abc(int n) => abc_r("", n);
Notice that the parameter n represents the number of choices that remain to be made, i.e. the number of string characters that we still must generate.
As another possibility, as the recursion descends we can push all choices we've made so far onto a stack. Once we have made N choices, we can print out the values on the stack. Each time the recursion returns, we pop our last choice off the stack, restoring its previous state. This solution might look like this:
void abc2(int n) {
Stack<char> stack = new Stack<char>();
void go(int n) {
if (n == 0)
WriteLine(string.Join("", stack.Reverse()));
else {
foreach (char c in "abc") {
stack.Push(c);
go(n - 1);
stack.Pop();
}
}
}
go(n);
}
In solution 1 above, we never have to undo a choice that we have made, because the expression 'result + c' creates a copy of the prefix string with the additional character c. The original prefix string remains unchanged (as it must be, since strings are immutable in C#). However, solution 2 may be slightly more efficient because it never copies the set of choices accumulated so far.
When we study larger problems that explore an exponential state space, we will often see this same choice: we may either (a) copy the state each time we recurse, or (b) modify the state before recursing, then undo the change afterwards.
We may actually solve the problem non-recursively, by extracting digits from an integer. To see how this will be possible, suppose that instead of the characters 'a', 'b' and 'c' we want to generate the digits 0, 1, and 2. Then our output for N = 3 will look like this:
000 001 002 010 011 012 020 021 022 100 101 …
This is simply all 3-digit numbers in base 3!
For a given N, there are 3N N-digit numbers in base 3, which is exactly the number of possible solutions that we saw before. So we may simply loop through integers from 0 to 3N – 1, extract a series of base-3 digits from each, and convert each such digit to a character 'a', 'b' or 'c'. Here is the code:
void abc3(int n) {
string convert(int i) {
string s = "";
for (int k = 0 ; k < n ; ++k) {
s = "abc"[i % 3] + s;
i = i / 3;
}
return s;
}
int p = (int) Math.Pow(3, n);
for (int i = 0 ; i < p ; ++i)
WriteLine(convert(i));
}The solutions above are top-down in that they accumulate a series of choices as the recursion depends. As a different approach, we may write a recursive function that returns a sequence of all possible solutions. Our function will call itself to generate a sequence of solutions for a subproblem, then transform each of those into some number of solutions to the top-level problem.
Notice the recursive structure of this 'abc' problem. In the tree above, we can see that to generate a solution for a given n, we must choose a first letter c (i.e. 'a', 'b', or 'c'), then recursively generate a solution s to the same problem with size (n - 1). That gives us a solution consisting of c prepended to s.
The natural base case for our recursion is n = 0. In this base case, should the function return an empty list, or a list with a single element?
For a clue to the answer, recall that there should be 3n output strings. Of course 30 = 1, so this suggests that we should return a list of length 1. Indeed, there is exactly one string of length 0 containing only characters from the set {'a', 'b', 'c'}, namely the empty string. Be careful when writing this sort of base case in a combinatorial problem. In this problem and many others, if you return an empty list in the base case (meaning that there is no solution) then the function will not work!
We can most easily write this bottom-up solution in a language with list comprehensions, such as Python:
def abc4(n):
if n == 0:
return ['']
return [c + s for c in 'abc' for s in abc4(n – 1)]
Unfortunately C# has no list comprehensions, so we can't write a bottom-up solution quite like this. However we can use another C# feature called iterators. So let's learn about iterators now, and then we'll return to this bottom-up abc solution.
In C# an iterator is
a function or method that contains one or more yield
return statements,
which produce an enumerable
sequence of values. Each time the caller asks for the
next value in the sequence, the function's code runs until it yields
the next value to the caller.
An iterator will return a value of type IEnumerable<T> for some type T, representing a sequence of values.
(By the way Python has a similar feature; however in Python these are called generators.)
Here is a simple iterator in C#:
IEnumerable<int> foo() {
yield return 3;
yield return 5;
yield return 7;
}
We may retrieve the values using a foreach loop, which consumes an enumerable sequence:
IEnumerable<int> vals = foo();
foreach (int i in vals)
WriteLine(i);
This will produce the output
3 5 7
Now let's modify our iterator to print some strings:
IEnumerable<int> foo() {
WriteLine("hello");
yield return 3;
WriteLine("hello again");
yield return 5;
WriteLine("yet again");
yield return 7;
}
And let's use it:
IEnumerable<int> vals = foo();
WriteLine("start");
foreach (int i in vals)
WriteLine(i);
This will produce the output
start hello 3 hello again 5 yet again 7
This output may come as a surprise. When we call the iterator function, it returns an enumerable sequence, but none of the code in the function has run yet. Each time we request a value from the sequence, the function runs until it yields a value, and then its execution is suspended until the next value is requested. This is quite different from any other control mechanism that we have seen thus far in either C# or Python!
Let's write an iterator that produces a sequence of squares 1, 4, 9, …, n2 for any given n:
# return a sequence of values 1, 4, 9, ..., n^2
def squares_to(n):
for i in range(1, n + 1): # 1, ..., n
yield i * i
Let's try it:
foreach (int i in squares_to(10))
WriteLine(i);
This produces
1 4 9 16 25 36 49 64 81 100
Let's write just the initial elements in a huge sequence of squares:
foreach (int i in squares_to(1_000_000_000)) {
WriteLine(i);
if (i > 50)
break;
}
This produces
1 4 9 16 25 36 49 64
Notice that the function runs quickly, even though the sequence is enormous. The program has not computed all values in the sequence; instead, the generator function squares_to() generates values on demand when and only if they are requested.
In fact, we may write a version of squares_to() that generates an infinite sequence of squares:
// return an infinite sequence of squares:
// 1, 4, 9, 16, ...
IEnumerable<int> all_squares() {
for (int i = 1 ; true ; ++i)
yield return i * i;
}
Now let's retrieve just the first few of those:
foreach (int i in all_squares()) {
WriteLine(i);
if (i > 20)
break;
}
This produces
1 4 9 16 25
As another example using infinite sequences, recall Project Euler's problem 2:
By considering the terms in the Fibonacci sequence whose values do not exceed four million, find the sum of the even-valued terms.
Let's write a solution using an iterator that generates an infinite sequence of Fibonacci numbers:
// return an infinite sequence of all Fibonacci numbers:
// 1, 1, 2, 3, 5, 8, ...
IEnumerable<int> fibs() {
int a = 1, b = 1;
while (true) {
yield return a;
(a, b) = (b, a + b);
}
}
int euler2() {
int sum = 0;
foreach (int f in fibs()) {
if (f > 4_000_000)
break;
if (f % 2 == 0) // f is even
sum += f;
}
return sum;
}Now that we know about iterators, let's use them to write a bottom-up solution to the abc problem. Once again, here is a solution using a list comprehension in Python:
def abc4(n):
if n == 0:
return ['']
return [c + s for c in 'abc' for s in abc4(n – 1)]
In C#, we may write
IEnumerable<string> abc4(int n) {
if (n == 0)
yield return "";
else
foreach (char c in "abc")
foreach (string s in abc4(n - 1))
yield return c + s;
}
This function will return an enumerable sequence of solutions.
Because we generated them using yield return,
they will be produced only on demand. Let's print the first few
solutions when n = 30:
int count = 5;
foreach (string s in abc4(30)) {
WriteLine(s);
if (--count == 0)
break;
}
This will produce
aaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaab aaaaaaaaaaaaaaaaaaaaaaaaaaaaac aaaaaaaaaaaaaaaaaaaaaaaaaaaaba aaaaaaaaaaaaaaaaaaaaaaaaaaaabb
The total number of solutions is 330, an enormous number, however the code above runs quickly since it only generates the first few.
Another typical combinatorial problem is generating all subsets of a set. Specifically, suppose that for any N we'd like to generate all subsets of the set {1, 2, …, N}. For N = 3, our output might look like this (in some order):
{ }
{ 1 }
{ 2 }
{ 1 2 }
{ 3 }
{ 1 3 }
{ 2 3 }
{ 1 2 3 }One way to view this problem is as a series of N choices, one for each of the values {1, 2, …, N}. In each choice, we decide whether a certain value will be absent from the set or present in it. Each of these N choices is a binary decision, and so there will be 2N possible solutions.
We can solve this problem using any of the 4 techniques that we saw above for the abc problem. Let's write a solution using a prefix parameter:
// recursive helper function
void subsets_r(string prefix, int i, int n) {
if (i > n)
WriteLine("{" + prefix + "}");
else {
subsets_r(prefix + i + " ", i + 1, n); // i is in the subset
subsets_r(prefix, i + 1, n); // i is not in the subset
}
}
void subsets(int n) => subsets_r(" ", 1, n);
Our decisions are binary, so our recursive function calls itself twice, once for each possible choice.
Let's run it:
subsets(4);
This will produce this output:
{ 1 2 3 4 }
{ 1 2 3 }
{ 1 2 4 }
{ 1 2 }
{ 1 3 4 }
{ 1 3 }
{ 1 4 }
{ 1 }
{ 2 3 4 }
{ 2 3 }
{ 2 4 }
{ 2 }
{ 3 4 }
{ 3 }
{ 4 }
{ }
We can solve a large number of problems using an exhaustive search. This means that we search through a problem space, looking for solutions - typically those which satisfy various constraints.
Typically our search will be recursive, so it will explore a tree of possibilities. However the shape of this tree may be different than in the combinatorial problems we saw above, because some parts of the tree will be cut off. That's because as we explore the tree, at some points there may be no decision we can make that will satisfy the problem's constraints. So at that point the search will backtrack and explore the next possibility. This approach is sometimes called a backtracking depth-first search.
A classic example of a problem that we can solve in this way is the N queens puzzle. Our goal is to place N queens on a chessboard such that none of them attack any other. Recall that queens in chess may move horizontally, vertically, or diagonally.
A moment's reflection will show that the puzzle has a trivial solution for N = 1, and no possible solutions for N = 2 or N = 3. Now let's think about how to search for a solution for N = 4.
Certainly we may only place one queen in any row. And, since we must place N queens, every row will need to contain a queen. So in this problem the first decision we may make is where to place the queen in the first row. After that, we can decide where to place the queen in the second row, and so on. As we explore this tree of possibilities, we will not consider all possible ways to place N queens in N rows (there are NN of those) since the search will only explore parts of the tree where all queens placed so far satisfy the constraints, i.e. don't attack each other.
Here is a partial search tree for N = 4:
In the leftmost two branches of this tree, the search gets cut off because there is no valid position in which to place a queen in the next row. The third branch leads to a solution. If we allow our search to continue past that point, it will find one more solution (which is a rotated version of this one).
Probably the easiest way to write this search in C# is to use a stack that holds the positions of all the queens placed so far. We could use a Stack<int>, or we can just use an array of type int[] that we will fill in as the recursion proceeds downward. With the array, there will be no need to pop when a recursive call returns; a leftover array entry will do no harm since it will be overwritten when the recursion proceeds downward again.
Here is an implementation using an array. It prints out only the first solution that it finds:
// Return true if queens at (x1, y1) and (x2, y2) attack each other.
bool attack(int x1, int y1, int x2, int y2) =>
x1 == x2 || y1 == y2 || Abs(x1 - x2) == Abs(y1 - y2);
void queens(int n) {
// The x-positions (0 .. n - 1) of queens placed in all rows so far.
int[] queens = new int[n];
// True if we can place a queen at (x, y) without attacking any queens above.
bool can_add(int x, int y) {
for (int y0 = 0; y0 < y ; ++y0)
if (attack(x, y, queens[y0], y0))
return false;
return true;
}
// Draw a solution to the puzzle.
void draw() {
for (int y = 0 ; y < n ; ++y) {
for (int x = 0 ; x < n ; ++x)
Write((queens[y] == x ? 'Q' : '.') + " ");
WriteLine();
}
WriteLine();
}
// Our recursive search function. Given that y queens have already been placed,
// it places the remaining queens (if possible) and prints a solution if found.
// Returns true if a solution was found.
bool go(int y) {
if (y == n) {
draw();
return true;
}
for (int x = 0 ; x < n ; ++x)
if (can_add(x, y)) {
queens[y] = x;
if (go(y + 1))
return true;
}
return false;
}
go(0);
}
Let's run this function to find a solution for N = 12. The call
queens(12);
produces this output:
Q . . . . . . . . . . . . . Q . . . . . . . . . . . . . Q . . . . . . . . . . . . . . Q . . . . . . . . . . . . . Q . . . . . . . . . . . . . Q . . . . . Q . . . . . . . . . . . . . . . . Q . . Q . . . . . . . . . . . . . . . . Q . . . . . . . . . . . . . Q . . . . . . Q . . . . . . . .