Introduction to Algorithms, 2022-3
Week 4: Notes

Sieve of Eratosthenes

We've seen in previous lectures that we can determine whether an integer n is prime using trial division, in which we attempt to divide n by successive integers. Because we must only check integers up to √n, this primality test runs in time O(√n).

Sometimes we may wish to generate all prime numbers up to some limit N. If we use trial division on each candidate, then we can find all these primes in time O(N √N). But there is a faster way, using a classic algorithm called the Sieve of Eratosthenes.

It's not hard to carry out the Sieve of Eratosthenes using pencil and paper. It works as follows. First we write down all the integers from 2 to N in succession. We then mark the first integer on the left (2) as prime. Then we cross out all the multiples of 2. Now we mark the next unmarked integer on the left (3) as prime and cross out all the multiples of 3. We can now mark the next unmarked integer (5) as prime and cross out its multiples, and so on. Just as with trial division, we may stop when we reach an integer that is as large as √N.

Here is the result of using the Sieve of Eratosthenes to generate all primes between 2 and 30:

23456789101112131415161718192021222324252627282930

We can easily implement the Sieve of Eratosthenes in Python:

prime = n * [True]           # initially assume all are prime
prime[0] = prime[1] = False  # 0 and 1 are not prime

for i in range(2, n):
    if prime[i]:
        # cross off multiples of i
        for j in range(2 * i, n, i):
            prime[j] = False

How long does the Sieve of Eratosthenes take to run?

The inner loop, in which we set prime[j] =False, runs N/2 times when we cross out all the multiples of 2, then N/3 times when we cross out multiples of 3, and so on. So its total number of iterations will be close to

N(1/2 + 1/3 + 1/5 + ... + 1/N)

The series of reciprocals of primes

1/2 + 1/3 + 1/5 + 1/7 + 1/11 + 1/13 + ...

is called the prime harmonic series. How can we approximate its sum through a given element 1/p?

Euler was the first to show that the prime harmonic series diverges: its sum grows to infinity, through extremely slowly. Its partial sum through 1/p is actually close to ln (ln n). This means that the running time of the Sieve of Eratosthenes is

O(N(1/2 + 1/3 + 1/5 + ... + 1/N)) = O(N log log N)

This is very close to O(N). (As always, we are assuming that arithmetic operations take constant time.)

By the way, here is a poem about the Sieve. (To "sublime" means to sublimate, i.e. to transform from a solid into a gas.)

Sift the twos and sift the threes,
The Sieve of Eratosthenes.
When the multiples sublime,
The numbers that remain are prime.

prime-counting function

The prime-counting function π is defined as follows: for any integer n, π(n) is the number of prime numbers that are less than or equal to n.

Let's modify our code above to compute π(i) for every i < n as it runs:

prime = n * [True]           # initially assume all are prime
prime[0] = prime[1] = False  # 0 and 1 are not prime

# pi[i] = the # of primes that are <= i
pi = [0] * n
count = 0

for i in range(2, n):
    if prime[i]:
        count += 1
        # cross off multiples of i
        for j in range(2 * i, n, i):
            prime[j] = False
    pi[i] = count

Now let's plot the function π(i). We will also draw a line from the first to the last point:

import matplotlib.pyplot as plt
…

plt.figure(figsize = (8, 8))
plt.plot(range(n), pi)
plt.plot([0, n - 1], [0, count])
plt.show()

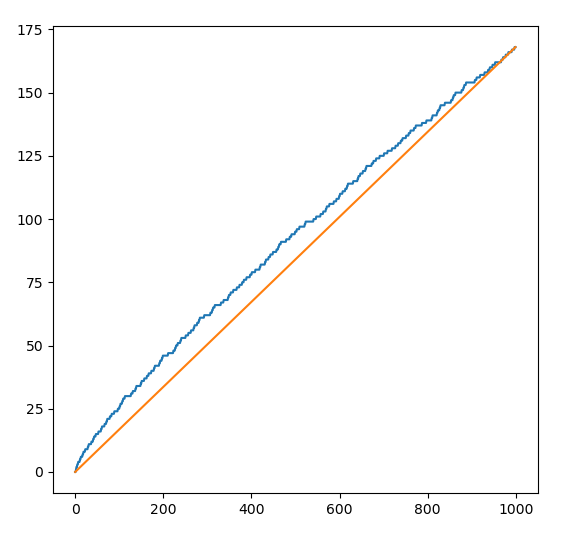
Here is the plot for n = 1000:

We see that the function π grows a bit more slowly than a linear function.

In fact, a famous result called the Prime Number Theorem states that

π(n) ~ n / ln n

Recall that ln n = log_e(n). The notation f(x) ~ g(x) means that as x goes to ∞ , f(x) / g(x) approaches 1.

So π(n) = O(n / log n). This function is nearly, but not quite, linear.

optimizing the Sieve

The Sieve of Eratosthenes is already very efficient, but we can optimize it slightly. When we cross off multiples of i, actually we can start at the value i², because any smaller multiples of i will already have been eliminated when we considered smaller values of i. That in turn means that we only need to consider values of i up to √n.

Here is an optimized version:

prime = n * [True]           # initially assume all are prime
prime[0] = prime[1] = False  # 0 and 1 are not prime

for i in range(2, int(sqrt(n)) + 1):
    if prime[i]:
        # cross off multiples of i
        for j in range(i * i, n, i):
            prime[j] = False

binary search

We may wish to search for a value (sometimes called the “key”) in a sorted array. We can use an algorithm called binary search to find the key efficiently.

Binary search is related to a well-known number-guessing game. In that game, one player thinks of a number N, say between 1 and 1,000. If we are trying to guess it, we can first ask "Is N greater than, less than, or equal to 500?" If we learn that N is greater, then we now know that N is between 501 and 1,000. In our next guess we can ask to compare N to 750. By always guessing at the midpoint of the unknown interval, we can divide the interval in half at each step and find N in a small number of guesses.

Similarly, suppose that we are searching for the key in a sorted array of 1,000 elements from a[0] through a[999] We can first compare the key to a[500]. If it is not equal, then we know which half of the array contains the key. We can repeat this process until the key is found.

To implement this in Python, we will use two integer variables lo and hi that keep track of the current unknown range. Initially lo = 0 and hi = length(a) - 1. At all times, we know that all array elements with indices < lo are less than the key, and all elements with indices > hi are greater than the key. That means that the key, if it exists in the array, must be in the range a[lo] … a[hi]. As the binary search progresses, lo and hi move toward each other. If eventually hi < lo, then the unknown range is empty, meaning that the key does not exist in the array.

Here is a binary search in Python. (Recall that a Python list is actually an array.)

# Search for value k in the list a.

lo = 0
hi = len(a)- 1

while lo <= hi:
    mid = (lo + hi) // 2
    if a[mid] == k:
        print('found', k, 'at index', mid)
        break
    elif a[mid] < k:
        lo = mid + 1
    else:  # a[mid] > k
        hi = mid - 1

Let's now consider the big-O running time of binary search. Suppose that the input array has length N. After the first iteration, the unknown interval (hi – lo) has approximately (N / 2) elements. After two iterations, it has (N / 4) elements, and so on. After k iterations it has N / 2^k elements. We will reach the end of the loop when N / 2^k = 1, so k = log₂(N). This means that in the worst case (e.g. if the key is not present in the array) binary search will run in O(log N) time. In the best case, the algorithm runs in O(1) since it might find the desired key immediately, even if N is large.

binary search for a boundary

Suppose that we know that a given array consists of a sequence of values with some property P followed by some sequence of values that do not have that property. Then we can use a binary search to find the boundary dividing the values with property P from those without it.

For example, suppose that we know that an array contains a sequence of non-decreasing integers. Given a value k, we want to find the index of the first value in the array that is greater than or equal to k. Because the array is non-decreasing, it must contain a sequence of values that are less than k, followed by a sequence of values that are at least k. We want to find the boundary point between these sequences.

# Given an array a of non-decreasing values, find the first one that is >= k.

lo = 0
hi = len(a) - 1

while lo <= hi:
  mid = (lo + hi) // 2
  if a[mid] < k:
    lo = mid + 1
  else:   # a[mid] >= k
    hi = mid - 1

print('The first value that is at least', k, 'is', a[lo])

At every moment as the function runs:

for i < lo: a[i] < k
for lo ≤ i ≤ hi: we don't know whether a[i] is less than or greater than k
for i > hi: a[i] ≥ k

When the while loop finishes, lo and hi have crossed, so lo = hi + 1. A this point there are no unknown elements, and the boundary we are seeking lies between hi and lo. Specifically:

For all i ≤ hi, a[i] < k
For all i ≥ hi + 1, a[i] ≥ k

And so lo = hi + 1 is the index of the first value greater than or equal to k.

This version of the algorithm runs in O(log N) in both the best and worst case, since the 'while' loop will never exit early.

As mentioned above, we can use this form of binary search with any property P, not just the property of being less than k. As another example, if we have an array that consists of a sequence of even integers followed by a sequence of odd integers, we can find the first odd integer using this algorithm.

square root using binary search

We can even use a binary search to solve some problems that don't involve finding elements in a list. For example, suppose that we want to compute the integer square root of n, i.e. the largest integer j such that j² ≤ n. (If n is a perfect square, j will be its actual square root.)

We can solve this problem using a binary search. j must be an integer in the range from 0 .. n. For all i ≤ j, i² ≤ n. For all i > j, i² > n. So this is essentially a binary search for a boundary, except that if we find the actual value j, we can exit early. Here is a solution:

def int_sqrt(n):
    lo = 0
    hi = n

    while lo <= hi:
        mid = (lo + hi) // 2
        if mid * mid == n:
            return mid
        if mid * mid <= n:
            lo = mid + 1
        else:
            hi = mid - 1
    
    # At this point hi == lo – 1.  The boundary lies between hi and lo.
    # hi is the square root, rounded down to the nearest integer.
    return hi

n = int(input('Enter n: '))
print(int_sqrt(n))