A graph consists of a set of vertices (sometimes called nodes in computer science) and edges. Each edge connects two vertices. In a undirected graph, edges have no direction: two vertices are either connected by an edge or they are not. In a directed graph, each edge has a direction: it points from one vertex to another. A graph is dense if it has many edges relative to its number of vertices, and sparse if it has few such edges. Some graphs are weighted, in which case every edge has a number called its weight.
Graphs are fundamental in computer science. Many problems can be expressed in terms of graphs, and we can answer many interesting questions using graph algorithms.
Often we will assume that each vertex in a graph has a unique id. Sometimes ids are integers; in a graph with V vertices, typically these integers will range from 0 through (V - 1). Here is one such undirected graph:
Alternatively, we may sometimes assume that vertex ids are strings, or belong to some other data type.
How may we store
a graph with V vertices in memory? As one possibility, we can use
adjacency-matrix representation. Assuming that each vertex has
an integer id, the graph will be
stored as a two-dimensional
array
g of booleans, with dimensions V
x V. In Python, g will be a list of
lists. In this
representation, g[i][j]
is true if and only there is an
edge from vertex i to vertex j.
If the graph is
undirected, then the adjacency matrix will be symmetric:
g[i][j]
= g[j][i]
for all i and j.
Here is an adjacency-matrix representation of the undirected graph above. Notice that it is symmetric:
graph = [
[False, True, True, False, False, True, True],
[True, False, False, False, False, False, False],
[True, False, False, False, False, False, False],
[False, False, False, False, True, True, False],
[False, False, False, True, False, True, True],
[True, False, False, True, True, False, False],
[True, False, False, False, True, False, False]
]Also notice that all the entries along the main diagonal are False. That's because the graph has no self-edges, i.e. edges from a vertex to itself.
Alternatively,
we can use
adjacency-list representation,
in which for each vertex we store an adjacency list,
i.e. a list of its adjacent
vertices. Assuming that vertex
ids are integers, then in
Python this representation will generally take the form of a list
of lists
of
integers. For a graph g, g[i]
is the
adjacency list of i, i.e. a list of ids of vertices adjacent to i.
(If the graph is directed, then more specifically g[i] is a list of
vertices to which there are edges leading from i.)
When we store an undirected graph in adjacency-list representation, then if there is an edge from u to v we store u in v’s adjacency list and also store v in u’s adjacency list.
Here is an adjacency-list representation of the undirected graph above:
graph = [
[1, 2, 5, 6], # neighbors of 0
[0], # neighbors of 1
[0], # …
[4, 5],
[3, 5, 6],
[0, 3, 4],
[0, 4]
]Now, the order of the vertices in each adjacency list does not matter. So we could actually store each list of neighbors as a Python set rather than a list; then the entire structure will be a list of sets of integers:
graph = [
{1, 2, 5, 6}, # neighbors of 0
{0}, # neighbors of 1
…However, if most vertices have only a small number of neighbors than a list representation will generally be more efficient.
Now suppose that vertex ids are not integers – for example, they may be strings, as in this graph:
Then in Python the adjacency-list representation will be a dictionary of lists. For example, the graph above has this representation:
graph = {
'c': ['f', 'q', 'x'],
'f': ['c', 'p', 'q', 'w'],
'p': ['f'],
'w': ['f', 'q', 'x'],
'x': ['c', 'w']
}Suppose that we have a graph with integer ids. Which representation should we use? Adjacency-matrix representation allows us to immediately tell whether two vertices are connected, but it may take O(V) time to enumerate a given vertex’s edges. On the other hand, adjacency-list representation is more compact for sparse graphs. With this representation, if a vertex has e edges then we can enumerate them in time O(e), but determining whether two vertices are connected may take time O(e), where e is the number of edges of either vertex. Thus, the running time of some algorithms may differ depending on which representation we use.
In this course we will usually represent graphs using adjacency-list representation.
In this course we will study two fundamental algorithms that can search a directed or undirected graph, i.e. explore it by visiting its nodes in some order.
The first of these algorithms is depth-first search, which is something like exploring a maze by walking through it. Informally, it works like this. We start at any vertex, and begin walking along edges. As we do so, we remember all vertices that we have ever visited. We will never follow an edge that leads to an already visited vertex. Each time we hit a dead end, we walk back to the previous vertex, and try the next edge from that vertex (as always, ignoring edges that lead to visited vertices). If we have already explored all edges from that vertex, we walk back to the vertex before that, and so on.
For example, consider this undirected graph that we saw above:
Suppose that we perform a depth-first search of this graph, starting with vertex 0. We might first walk to vertex 1, which is a dead end. The we backtrack to 0 and walk to vertex 2, which is also a dead end. Now we backtrack to 0 again and walk to vertex 5. From there we might proceed to vertex 3, then 4. From 4 we cannot walk to 5, since we have been there before. So we walk to vertex 6. From 6 we can't proceed to 0, since we have been there before. So we backtrack to 4, then back to 3, 5, and then 0. The depth-first search is complete, since there are no more edges that lead to unvisited vertices.
As a depth-first search runs, we may imagine that at each moment every one of its vertices is in three possible states:
A vertex is undiscovered if we have not yet seen it.
A vertex V is on the frontier if we have seen it, and are still exploring some part of the graph that we reached through an edge leading from V. In other words, we will backtrack to V at some future time.
A vertex is explored if we have left it because we have fully explored all possible paths leading from it, so we will not backtrack to it again.
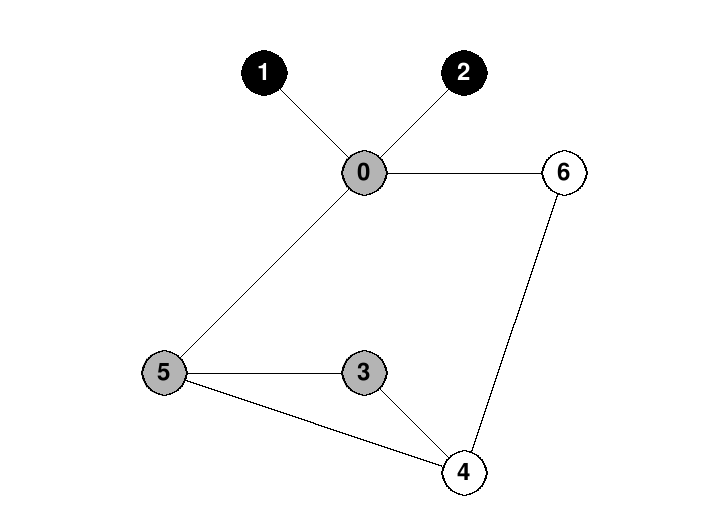
Often when we draw pictures of a depth-first search (and also of some other graph algorithms), we draw undiscovered vertices in white, frontier vertices in gray and explored vertices in black.
For example, here is a picture of a depth-first search in progress on the graph above. The search started at vertex 0, went to vertex 1, then backtracked back to 0. Then it went to vertex 2 and backtracked back to 0 again. Then it proceeded to vertex 5, and has just arrived at vertex 3:
Here's a larger graph, with vertices representing countries in Europe. The graph contains edges between countries that either border each other or are reachable from each other by a direct ferry (in which case the edges are depicted as dashed lines):
Here's a picture of a depth-first search in progress on this graph. The search started with Austria, and has now reached Italy:
It is easy to implement a depth-first search using a recursive function. In fact we have already done so in this course! For example, we wrote a function to add up all values in a binary tree, like this:
def sum(n):
if n == None:
return 0
return sum(n.left) + n.val + sum(n.right)
This function actually visits all tree nodes using a depth-first tree search.
For a depth-first search on arbitrary graphs which may not be trees, we must avoid walking through a cycle in an infinite loop. To accomplish this, as described above, when we first visit a vertex we mark it as visited. Whenever we follow an edge, if it leads to a visited vertex then we ignore it.
If a graph has vertices numbered from 0 to (V – 1), we may efficiently represent the visited set using an array of V boolean values. Each value in this array is True if the corresponding vertex has been visited.
Here is Python code that implements a depth-first search using a nested recursive function. It takes a graph g in adjacency-list representation, plus a vertex id 'start' where the search should begin. It assumes that vertices are numbered from 0 to (V – 1), where V is the total number of vertices.
# recursive depth-first search over graph with integer ids
def dfs(g, start):
visited = [False] * len(g)
def visit(v):
print('visiting', v)
visited[v] = True
for w in g[v]: # for all neighbors of vertex v
if not visited[w]:
visit(w)
visit(start)
This function merely prints out the visited nodes. But we can modify it to perform useful tasks. For example, to determine whether a graph is connected, we can run a depth-first search and then check whether the search visited every node. As you will see in more advanced courses, a depth-first search is also a useful building block for other graph algorithms: determining whether a graph is cyclic, topological sorting, discovering strongly connnected components and so on.
This depth-first search does a constant amount of work for each vertex (making a recursive call) and for each edge (following the edge and checking whether the vertex it points to has been visited). So it runs in time O(V + E), where V and E are the numbers of vertices and edges in the graph.
As another example, let's run a depth-first search on the undirected graph of Europe that we saw above. Here is a file 'europe' containing data that we can use to build the graph. The file begins like this:
austria: germany czech slovakia hungary slovenia italy belgium: netherlands germany luxembourg france bulgaria: romania greece …
And here is a function that can read this file to build an adjacency-list representation in memory:
# read graph in adjacency list representation
def read_graph(file):
g = {}
def add(v, w):
if v not in g:
g[v] = []
g[v].append(w)
with open(file) as f:
for line in f:
source, dest = line.split(':')
if source not in g:
g[source] = []
for c in dest.split():
add(source, c)
add(c, source)
return gHere is a function that will perform the depth-first search. Since vertex ids are strings, we can't represent the visited set using an array of booleans as we did above; instead, we use a Python set.
# recursive depth-first search over graph with arbitrary ids
def dfs(g, start):
visited = set()
def visit(v, depth):
print(' ' * depth + v)
visited.add(v)
for w in g[v]:
if w not in visited:
visit(w, depth + 1)
visit(start, 0)The recursive helper function visit() uses an extra parameter 'depth' to keep track of the search depth. When it prints the id of each visited vertex, it indents the output by 2 spaces for each indentation level. Let's run the search:
>>> europe = read_graph('europe')
>>> dfs(europe, 'ireland')
ireland
uk
france
belgium
netherlands
germany
austria
czech
poland
lithuania
latvia
estonia
finland
sweden
denmark
slovakia
hungary
croatia
slovenia
italy
greece
bulgaria
romania
malta
luxembourg
spain
portugal
>>> The indentation reveals the recursive call structure. We see that from the start vertex 'ireland' we recurse all the way down to 'denmark', then backtrack to 'poland' and begin exploring through 'slovakia', and so on.
Even with these changes to work with arbitary vertex ids, our depth-first search code still runs in O(V + E), since dictionary and set operations in Python (e.g. looking up an element in a dictionary, or checking whether an element is present in a set) run in O(1) on average.
We will now look at breadth-first search, which is another fundamental graph algorithm.
Starting from some vertex V, a breadth-first search first visits vertices adjacent to V, i.e. vertices of distance 1 from V. It then visits vertices of distance 2, and so on. In this way it can determine the shortest distance from V to every other vertex in the graph.
We can implement a breadth-first search using a queue. Let's suppose that we have a Queue class with operations enqueue() and dequeue(). (As one possibility, we can implement this class using a linked list, as we've seen in earlier lectures.) Also, just as with a depth-first search, we will need a visited set to avoid walking in circles as we search.
We begin by adding the start vertex to the queue and marking it as visited. In a loop, we repeatedly remove vertices from the queue. Each time we remove a vertex, we mark all of its adjacent unvisited vertices as visited and add them to the queue. The algorithm terminates once the queue is empty, at which point we will have visited all reachable vertices.
For example, consider the graph of Europe that we saw above:
Suppose that we begin a breadth-first search at 'austria'. Initially the queue contains only that vertex:
Q = austria
We dequeue 'austria' and enqueue its neighbors (and add them to the visited set):
Q = germany czech hungary slovakia slovenia
Next, we dequeue 'germany' and add its neighbors to the queue. However we do not add 'austria' or 'czech', which have already been visited:
Q = czech hungary slovakia slovenia belgium netherlands luxembourg denmark poland france
Now we dequeue 'czech'. Its neighbors are 'austria', 'germany', 'poland' and 'slovakia' but they are all visited, so there is nothing to add:
Q = hungary slovakia slovenia belgium netherlands luxembourg denmark poland france
Now we dequeue 'hungary'. It has two unvisited neighbors 'romania' and 'croatia', so we enqueue them:
Q = slovakia slovenia belgium netherlands luxembourg denmark poland france romania croatia
Next, we dequeue 'slovakia' and 'slovenia'. They have no unvisited neighbors:
Q = belgium netherlands luxembourg denmark poland france romania croatia
Just as with a depth-first search, we may imagine that at any time during a breadth-first search, each vertex is either undiscovered (white), on the frontier (gray) or explored (black). The queue represents the frontier, i.e. the gray vertices. So the picture now looks like this:
The gray vertices are in the queue; the black vertices have already been dequeued; the white vertices have not yet entered the queue.
As the algorithm runs, all vertices in the queue are at approximately the same distance from the start vertex. To be more precise, at every moment in time there is some value d such that all vertices in the queue are at distance d or (d + 1) from the start vertex. (At this particular moment in this example, all the vertices in the queue have distance either 1 or 2 from the start vertex 'austria'.)
Here's an implementation of breadth-first search for a graph with integer ids. The visited set is an array of booleans:
# breadth-first search over graph with integer ids
def bfs(graph, start):
visited = [False] * len(graph)
q = Queue()
visited[start] = True
q.enqueue(start)
while not q.is_empty():
v = q.dequeue()
print('visiting', v)
for w in graph[v]:
if not visited[w]:
visited[w] = True
q.enqueue(w)
Notice that we mark vertices as visited when we add them to the queue, not when we remove them. This ensures that our algorithm will not add the same vertex to the queue more than once.
Like a depth-first search, this breadth-first search function does a constant amount of work for each vertex and edge, so it also runs in time O(V + E).
Let's modify our breadth-first search code so that it can run on our graph of Europe. Since vertex ids are strings, we will store the visited set using a Python set, not an array of booleans. Also, as we search we will compute the distance from the start vertex to every other vertex that we reach. To achieve this, each queue element will be a pair (v, d), where v is a vertex id and d is the distance from the start vertex to v. Finally, when we print out each vertex we will indent it by its distance from the start. Here is the code:
# breadth-first search over graph with arbitrary ids
def bfs(g, start):
visited = set()
q = Queue()
q.enqueue((start, 0))
visited.add(start)
while not q.is_empty():
(v, dist) = q.dequeue()
print(' ' * dist + v)
for w in g[v]:
if w not in visited:
q.enqueue((w, dist + 1))
visited.add(w)Let's run it:
>>> bfs(europe, 'ireland')
ireland
uk
france
belgium
luxembourg
germany
italy
spain
netherlands
austria
czech
denmark
poland
greece
malta
slovenia
portugal
slovakia
hungary
sweden
lithuania
bulgaria
croatia
romania
finland
latvia
estonia
>>> We can easily see that the breadth-first search discovers vertices in increasing order of distance from the start vertex.
Depth-first search and breadth-first search are fundamental algorithms for exploring graphs. Actually these algorithms are more broadly applicable: we can use them to solve many problems in which we search through a state space. These problems have a graph-like structure. In each such problem, there is an initial state and a function that maps each state to a list of its possible successor states. We are searching for some path that leads from the initial state to a goal state.
For example, consider the problem of finding the shortest number of hops that a knight can make to travel from one square to another on a chessboard. Recall that a knight's move has an L shape. The following picture indicaes the 8 different squares to which a knight at the given position can move:

In this problem, each state is an (x, y) position on the board. The initial state is the knight's starting square. Each state has up to 8 neighbors, which are the squares that the knight can move to next. The goal state is the position that the knight is trying to reach.
We may solve this problem using a breadth-first search. (A depth-first search would not work, since we are looking for a shortest path.) In fact we need to modify our last breadth-first search function only slightly. Each queue element will be a triple (x, y, dist), where dist is the shortest distance between the starting square and the position (x, y). To compute the neighboring states of each state, we will loop over all possible 8 directions in which a knight may move. Here is an implementation:
dirs = [(1, 2), (-1, 2), (1, -2), (-1, -2),
(2, 1), (2, -1), (-2, 1), (-2, -1)]
# Print the smallest number of knight moves to get from (start_x, start_y)
# to (end_x, end_y) on a chessboard.
def knight_path(start_x, start_y, end_x, end_y):
# visited set = 8 x 8 array of booleans
# visited[x][y] is True if we have visited (x, y)
visited = [[False] * 8 for i in range(8)]
q = Queue()
q.enqueue( (start_x, start_y, 0) )
visited[start_x][start_y] = True
while not q.is_empty():
x, y, dist = q.dequeue()
print(f'visiting {(x, y)}')
if (x, y) == (end_x, end_y):
print(f'shortest distance is {dist}')
return
for dx, dy in dirs:
x1, y1 = x + dx, y + dy # next position
if 0 <= x1 < 8 and 0 <= y1 < 8 and not visited[x1][y1]:
q.enqueue( (x1, y1, dist + 1) )
visited[x1][y1] = True
print('unreachable')As an exercise, you could enhance this function so that it prints out a sequence of positions along the shortest path from the start to the end position.