Consider the following game. There is a row of N coins on the table, with values V1, V2, ... VN. On each player's turn, they can take either the first coin in the row or the last coin in the row. Write a method that takes an array with the values of the coins, and returns the maximum amount of money that the first player can win if both players play optimally.
Consider the following game. Let W be a set of words, each containing only lowercase letters from 'a' to 'z'. Two players take turns adding a letter to a string S, which is initially empty. A player loses if after their turn either
they have made a word (i.e. S is a word in W), or
no more words are possible (i.e. S is not a prefix of any word in W).
For example, suppose that W = { "chirp", "cat", "dark", "dog", "donate", "donut" }. The game might proceed as follows:
A chooses d
B chooses o
A chooses n
B chooses u
Now A has lost: if he chooses 't' he has made the word 'donut', and he cannot choose any other letter since then no other word will be possible.
Write a program that can play Ghost. Read the list of possible English words from this file. Only use words that consist only of lowercase letters a-z from the Latin alphabet. Your program should be able to play either as player 1 or 2.
Can you defeat your own program? If not, make it easier by modifying your program to choose its first move randomly from the set of all possible moves that don't lose immediately.
Here is a GTK program that implements the game of Tic Tac Toe. Add an AI player using the minimax algorithm.
Here is a GTK program that implements the game of Connect Four. It includes two computer players: one (Greedy) with a certain strategy, and another (MyStrategy) that moves randomly. Improve MyStrategy so that it can beat Greedy at least 75% of the time.
Implement the game of Hex, with a user interface in GTK. Use a model-view architecture.
Implement an AI player for Hex.
Write an application that displays a bouncing ball. The ball should lose a bit of velocity each time it hits the ground, so that it eventually comes to a stop.
Extend the previous application so that the user can create new balls by clicking the mouse. Each ball should have a random size and color. All the balls should bounce simultaneously.
Write a program that displays a black background with 50 random stars, which appear as small white dots.
Extend the previous program so that a triangular spaceship appears at the center of the starfield. The user should be able to rotate the ship by holding down the left and right arrow keys.
Extend the previous program so that the spaceship can move. If the user holds the up arrow key, the ship should accelerate forward in the direction that it's currently pointing. If they release it, the ship should decelerate until it comes to a halt.
12. Longest Path
Consider the following representation for directed weighted graphs. This class represents edges:
class Edge {
public int dest; // destination
public double weight;
}
We can represent a graph in adjacency-list representation by a jagged
array of type Edge[][]. If g is an array of this type,
then g[i] is a subarray of edges leading from the i-th vertex.
Write a method int[] longest(Edge[][] graph,
int start, int end) that takes a directed acyclic graph
and finds the longest weighted path from vertex start
to vertex end. The method should return a list of
vertices along the path, including start and end.
If no path exists between the vertices, return null.
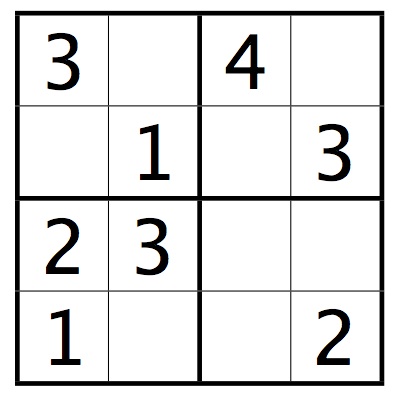
A mini-Sudoku puzzle looks like this:

To solve the puzzle, you must place a number from 1 to 4 in every square so that the numbers in every row, column, and mini-square are distinct.
Write a method that reads a mini-Sudoku puzzle from standard input. Empty squares will be represented by the number 0:
3040 0103 2300 1002
The method should print out a solution to the puzzle if it can find one, otherwise null.
Write a method that takes an undirected graph G (represented as a jagged array) with vertices numbered 1 .. N. The method should return the length of the longest path from vertex 1 to vertex N. A path cannot cannot contain the same vertex twice. No efficient algorithm is known for solving this problem, so you will need to perform an exhaustive search of all possible paths.