Week 1: Exercises

1. Fibonacci Sum

The Fibonacci numbers are

1, 1, 2, 3, 5, 8, 13, 21, …

Write a program that reads an integer N on a single line, and writes the sum of the first N Fibonacci numbers.

2. Number Wheel

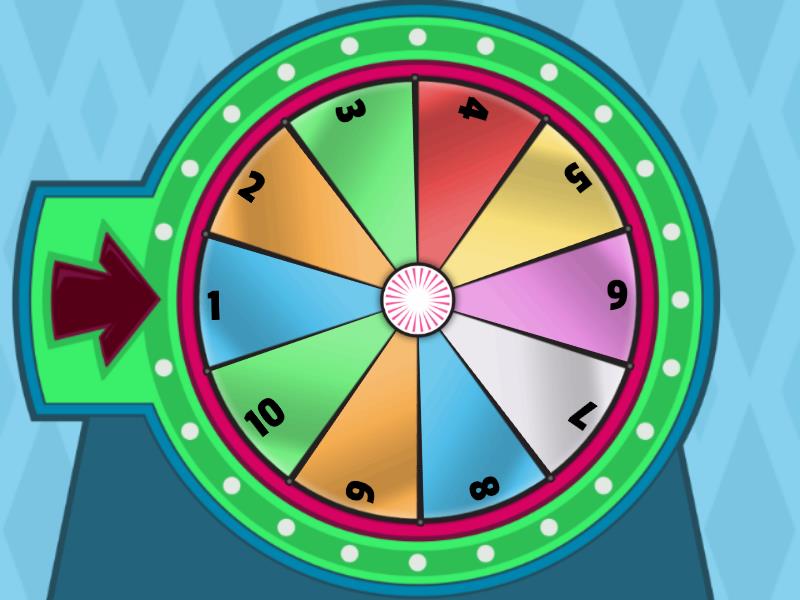
Consider this wheel with 10 numbers:

Write a program that reads two integers S and N on separate lines. S is the starting position of the wheel. N is a number of positions to turn the wheel, where a positive number indicates a counterclockwise rotation and a negative number is a clockwise rotation.

The program should print a single integer indicating the final position of the wheel.

3. Prime Counting

In number theory, the prime-counting function π(x) denotes the number of prime numbers that are less than or equal to x. (It is unrelated to the number π.)

a) Write a C# program that computes and prints π(1,000,000). Use trial division for primality testing.

b) Write the same program in Python.

c) Compare the running time of the two programs.

4. Sum of Ints

Consider this C# program:

        int sum = 0;
        for (int i = 1 ; i != 0; ++i)
            sum += i;
        Console.WriteLine(sum);

What value do you think it will print? Why?

5. Last Digits

Write a program that computes and prints the last 5 digits of the integer 2¹⁰⁰⁰.

6. Primality Claim

Consider this claim:

For every integer n ≥ 2, n is prime if and only if 2ⁿ – 2 is divisible by n.

For example:

• n = 2: 2² – 2 = 4 – 2 = 2 is divisible by 2

• n = 3: 2³ – 2 = 8 – 2 = 6 is divisible by 3

• n = 4: 2⁴ – 2 = 16 – 2 = 14 is not divisible by 4

• n = 5: 2⁵ – 2 = 32 – 2 = 30 is divisible by 5

We see that the claim is true at least through n = 5.

Write a C# program that determines whether the claim is true for all values through n = 1000. If the claim fails for any such n, print its value.

7. More Last Digits

Write a program that computes and prints the last 5 digits of the integer 3^k, where k = 2¹⁰⁰⁰.

8. Sum of Squares

Consider this C# program:

        int sum = 0;
        for (int i = 1 ; i != 0; ++i)
            sum += i * i;
        Console.WriteLine(sum);

What value do you think it will print? Why?