Testing is the process of trying to discover bugs in a program and, as far as is possible, ensure that it is bug-free.
The most basic way to test your program is manually, i.e. by running it and manually entering input or using it interactively. This generally doesn't scale well to larger programs. It's also difficult to test a program thoroughly in this way.
In recent decades there has been a major trend toward automated testing. One common form of automated testing is unit tests, which test individual pieces of functionality such as individual modules, classes, methods and/or functions inside a program.
In Python, we can easily write simple unit tests using the 'assert' statement. For example, suppose that we've written a class PriorityQueue with methods add(x), remove_smallest() and is_empty(). Here is a function with several unit tests for this class:
def test_queue():
pq = PriorityQueue()
assert pq.is_empty()
vals = [5, 3, 8]
for x in vals:
pq.add(x)
for x in [3, 5, 8]:
assert pq.remove_smallest() == x
assert pq.is_empty()
random.seed(0)
nums = [random.randrange(1000) for _ in range(100)]
for x in nums:
pq.add(x)
for x in sorted(nums):
assert pq.remove_smallest() == x
assert pq.is_empty()If any unit test in this function fails, the program will terminate with a stack trace revealing which test caused the problem.
Notice that one section of the code above calls the add() method with a series of random values. Random data of this sort can be very useful for testing. The function also calls random.seed(0), which ensures that random values will be the same on each run. That means that test results will be reproducible, which is a good thing.
It's often a good idea to run all unit tests automatically each time a program is run. That ensures that you'll notice immediately if a change to the program causes a unit test to fail.
By contrast, integration tests test the functionality of groups of modules or the entire program, e.g. by sending input to the program and checking its output.
If a program has a graphical interface, it might not be so easy to test it in an automated way. However, if you write your program using a model-view architecture then you should be able to write automated unit tests for the model portion of your program at least.
Companies that develop software generally spend a lot of time and energy on testing, and often encourage programmers to write lots of unit tests. Some people have even adopted the practice of test-driven development, in which programmers write unit tests for a function or class before they implement it.
To be very sure that software (or hardware) has no bugs, it is possible to write a mathematical proof of correctness of a piece of software (or hardware), and to check the proof in an automated way. However this is relatively expensive and difficult, so it's not done so often in practice. Making this easier is an active area of research.
We can use recursion to solve many problems of a combinatorial nature, such as generating subsets, combinations, or permutations of a set. In these problems, we use recursion to explore an exponential tree of possibilities. Sometimes this is called an an exhaustive search. In some such problems we will accept all possibilities that we discover, and in others we only want those that satisfy certain constraints.
As a first example, let's suppose that we'd like
write a function that
takes an integer n and
prints out all possible strings of length n containing only
characters from the set {'a', 'b',
'c'}. For example, if n = 2
then we will print these
strings:
aa ab ac ba bb bc ca cb cc
And if n = 3:
aaa aab aac aba abb abc aca acb acc baa bab bac …
There will be 3n strings in the output list. That's because there are 3 possible choices for the first letter, 3 for the second letter, and so on for each of the n letters.
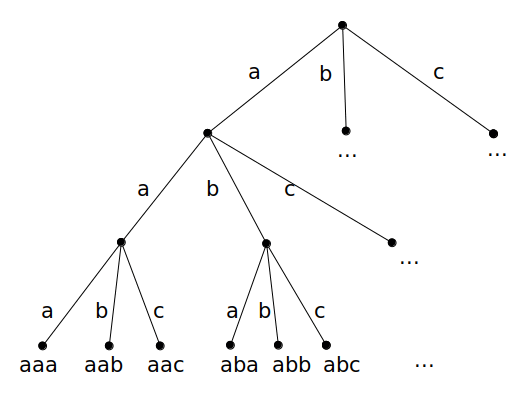
We can imagine a series of choices that we must make as we choose a string to print out. We can draw these in a tree. For example, if n = 3:

At each step, we choose the letter 'a', 'b' or 'c'. Affter we have made N choices, we have a string that we can print.
Any algorithm that can generate these strings for any given N will surely take exponential time, since the length of the output is exponential in N. This is a sign that we will probably need to use recursion to solve this problem, since a set of loops without recursion will generally run in polynomial, not exponential, time.
We will study 4 different solutions to this problem. Each of them will use a different technique that we may apply to other problems as well.
We can recursively explore this tree of choices. As the recursion descends, we will accumulate all choices we've made so far and pass them as a parameter to the next level of the recursion. When we have made N choices, we will print out the string we have built.
Here is our solution:
def abc1(n):
def go(result, i):
if i == 0: # we're at a leaf
print(result)
else:
for c in 'abc':
go(result + c, i - 1)
go('', n)
Notice that the parameter 'n' represents the number of choices that remain to be made, i.e. the number of string characters that we still must generate.
As another possibility, as the recursion descends we can push all choices we've made so far onto a stack. Once we have made N choices, we can print out the values on the stack. Each time the recursion returns, we pop our last choice off the stack, restoring its previous state. This solution might look like this:
def abc2(n):
stack = [] # stack of characters
def go(i):
if i == 0:
print(''.join(stack))
else:
for c in 'abc':
stack.append(c) # push onto stack
go(i - 1)
stack.pop() # pop off top
go(n)In solution 1 above, we never have to undo a choice that we have made, because the expression 'result + c' creates a copy of the string 'result' with the additional character c. The original string 'result' remains unchanged (as it must be, since strings are immutable in Python). However, solution 2 may be slightly more efficient because it never copies the set of choices accumulated so far.
When we study larger problems that explore an exponential state space, we will often see this same dichotomy: we may either (a) copy the state each time we recurse, or (b) modify the state before recursing, then undo the change afterwards.
The solutions above are top-down in that they accumulate a series of choices as the recursion depends. As a different approach, we may write a recursive function that returns a list of all possible solutions. Our function will call itself to generate a list of solutions for a subproblem, then transform each of those into some number of solutions to the top-level problem.
Notice the recursive structure of this 'abc' problem. Specifically, consider the list of output strings for n = 3:
aaa aab aac aba abb abc ...
If we look at only the last two characters of each string, we see the strings aa, ab, ac, ba and so on, which is precisely the list of strings for n = 2. In other words, each string for n = 3 consists of a character 'a', 'b', or 'c' followed by some string generated by the same function with n = 2.
The natural base case for our recursion is n = 0. In this base case, should the function return an empty list, or a list with a single element?
For a clue to the answer, recall that there should be 3n output strings. Of course 30 = 1, so this suggests that we should return a list of length 1. Indeed, there is exactly one string of length 0 containing only characters from the set {'a', 'b', 'c'}, namely the empty string. Be careful when writing this sort of a base case in a combinatorial problem. In this problem and many others, if you return an empty list in the base case (meaning that there is no solution) then the function will not work!
Here, then, is a recursive bottom-up solution:
def abc3(n):
# base case
if n == 0:
return ['']
# recursive case
l = []
for c in 'abc':
for s in abc3(n - 1):
l.append(c + s)
return lAlternatively, we may use a list comprehension to achieve the same result:
def abc3(n):
if n == 0:
return ['']
return [c + s for c in 'abc' for s in abc3(n – 1)]As a final possibility, we may solve the problem non-recursively, by extracting digits from an integer. To see how this will be possible, suppose that instead of the characters 'a', 'b' and 'c' we want to generate the digits 0, 1, and 2. Then our output for N = 3 will look like this:
000 001 002 010 011 012 020 021 022 100 101 …
This is simply all 3-digit numbers in base 3!
For a given N, there are 3N N-digit numbers in base 3, which is exactly the number of possible solutions that we saw before. So we may simply loop through integers from 0 to 3N – 1, extract a series of base-3 digits from each, and convert each such digit to a character 'a', 'b' or 'c'. Here is the code:
def abc4(n):
for i in range(0, 3 ** n):
s = ''
for j in range(n): # extract j digits from the number
d = i % 3 # extract a digit: 0, 1, or 2
s = 'abc'[d] + s # prepend to s
i = i // 3
print(s)Another typical combinatorial problem is generating all subsets of a set. Specifically, suppose that for any N we'd like to generate all subsets of the set {1, 2, …, N}. For N = 3, our output might look like this (in some order):
[] [1] [2] [1, 2] [3] [1, 3] [2, 3] [1, 2, 3]
One way to view this problem is as a series of N choices, one for each of the values {1, 2, …, N}. In each choice, we decide whether a certain value will be absent from the set or present in it. Each of these N choices is a binary decision, and so there will be 2N possible solutions.
Here is a solution using the stack technique that we saw above:
def subsets_stack(n):
stack = []
def go(i):
if i > n: # we have made all decisions
print(stack)
else:
# i might not be in the solution
go(i + 1)
# i might be in the solution
stack.append(i) # so include it
go(i + 1)
stack.pop() # go back to previous state
go(1)Here is a bottom-up solution. Once again, note that when N = 0 there is one solution (i.e. because 20 = 1), namely the empty set, so we must return it in our base case:
# Return a list of all the subsets of { 1, ..., n }, e.g.
# [ [], [1], [2], [1, 2]]
def subsets(n):
if n == 0:
return [ [] ]
else:
results = []
for s in subsets(n - 1): # for each subproblem solution s
results.append(s) # use s itself
results.append(s + [n]) # also include n
return resultsOr, using a list comprehension:
# Return a list of all the subsets of { 1, ..., n }.
def subsets(n):
if n == 0:
return [ [] ]
else:
return [t for s in subsets(n - 1) for t in [s, s + [n]] ]Here's a non-recursive solution that works by extracting binary digits:
def subsets(n):
for i in range(2 ** n):
# Imagine that i is a number in base 2.
# Each bit is 0 (that element is not in the subset) or 1 (it is in it).
s = []
for j in range(n): # extract n bits
b = i % 2 #one bit
if b == 1:
s.append(j + 1)
i //= 2
print(s)Another classic combinatorial problem is to generate all permutations of a string.
For example, if the input string is 'abc', the output will include these values:
abc acb bac bca cab cba
If the input string is 'abcd', the output will begin with these values:
abcd abdc acbd acdb adbc adcb bacd badc bcad …
If the length of the input string is N, then there will be N! output values, since there are N! permutations of a list of length N.
Let's study the recursive structure of the problem. Look at the permutations of 'abcd' above. Notice that the first 6 permutations consist of the character 'a' plus some permutation of 'bcd'. The next 6 permutations consist of the character 'b' plus some permutation of 'acd', and so on. We see that to generate a permutation of a string s, we must first choose some first character c. Then we can generate the remainder of the permutation, which will be any permutation of (s – c), i.e. the string obtained by deleting c from s.
Here's a solution using the stack technique that we saw above:
# Return a copy of 's' without the character at s[i].
def delete_at(s, i):
return s[:i] + s[i + 1:]
# Print all permutations of the string s.
def perm(s):
stack = []
# t = characters that still remain to choose from
def go(t):
if t == '':
print(''.join(stack))
else:
for i in range(len(t)): # for each possible index
stack.append(t[i])
go(delete_at(t, i)) # t without the character t[i]
stack.pop()
go(s)Here's a bottom-up solution:
# Return a list of all permutations of 's'.
def perm(s):
if s == '':
return ['']
results = []
for i in range(len(s)): # for each possible index
c = s[i] # grab one character
for t in perm(delete_at(s, i)):
results.append(c + t)
return resultsOr, using a list comprehension:
# Return a list of all permutations of 's'.
def perm(s):
if s == '':
return ['']
return [s[i] + t for i in range(len(s)) for t in perm(delete_at(s, i))]