Week 1: Exercises

1. Mortal Men

1. Write Prolog clauses expressing the following facts:

   • Socrates is a man.
   • Plato is a man.
   • All men are mortal.

2. Write Prolog queries asking the following questions:

   • Is Socrates a man?
   • Is Plato mortal?
   • Who is mortal?
   • Who is a man and is also mortal?
   • Do two different men exist?

2. Single Clause

1. Write a single clause that is equivalent to all the of the following facts:

   parent(charles, wenceslaus).
   parent(charles, margaret).
   parent(charles, sigismund).

2. Write a single clause that is equivalent to all the of the following facts:

parent(charles, wenceslaus).
parent(charles, margaret).
parent(charles, sigismund).
parent(sigismind, elizabeth).

3. Dancing Pairs

Consider this Prolog program:

male(hans).
male(charles).

female(elizabeth).
female(kate).

dance(P, Q) :- male(P), female(Q).

What answers will these queries produce, and in what order?

1. dance(charles, X).
2. dance(jacob, radka).
3. dance(kate, X).
4. dance(X, elizabeth).
5. dance(X, X).
6. dance(hans, elizabeth).
7. dance(X, john).
8. dance(X, Y).

4. Drinking Pairs

Consider this Prolog program:

drinks(thomas, whiskey).
drinks(sonya, beer).
drinks(lucy, wine).
drinks(radek, beer).
drinks(jarda, beer).

pair(P, Q, D) :- drinks(P, D), drinks(Q, D).

What answers will these queries produce, and in what order?

1. pair(P, thomas, whiskey).
2. pair(sonya, jarda, beer).
3. pair(thomas, sonya, beer).
4. pair(radek, radek, beer).
5. pair(X, Y, beer).
6. pair(X, Y, Z).

5. Termination

Consider this predicate:

foo(a).
foo(b).
foo(X) :- foo(X).

1. Consider the following queries. What answer(s) will they produce? Will they terminate?

• foo(Y).

• foo(Y), true.

• foo(Y), false.

• true, foo(Y).

• false, foo(Y).
  

2. Suppose that we move the rule to the top:
   
   foo(X) :- foo(X).
foo(a).
foo(b).
   
   Now what answer(s) will be produced by the query 'foo(Y)'?

6. Directed Graph

Consider this acyclic directed graph:

We can write a Prolog predicate representing adjacency between vertices:

edge(a, b).
edge(a, e).
edge(b, c).
edge(b, f).
edge(e, d).
edge(e, f).
edge(f, c).
edge(g, d).
edge(g, h).
edge(h, f).

1. Write a predicate path(V, W) that is true if there is some path from V to W in the directed graph.

2. Given your predicate, what answers will each of these queries produce?

   • path(f, f).
   • path(a, c).
   • path(g, e).
   • path(g, X).
   • path(X, h).
   • path(X, X).
   • path(X, Y).

7. Family Tree

Suppose that we define a family tree using predicates male, female and parent:

male(john). male(charles). male(wenceslaus).

female(anne). female(elizabeth).

parent(wenceslaus, anne). parent(wenceslaus, charles).
parent(charles, john). parent(charles, elizabeth).
...

Write Prolog predicates expressing the following relationships:

1. grandmother(G, X)

2. sibling(X, Y)

   Two people are siblings if they have at least one parent in common.

3. full_sibling(X, Y)

   Full siblings share both parents.

4. first_cousin(X, Y), second_cousin(X, Y)

   First cousins have parents who are full siblings. Second cousins have parents who are first cousins.

5. cousin(X, Y)

   Two people are cousins if they are N^th cousins for any N ≥ 1.

8. Map of Europe

Consider a map that shows 7 countries in central Europe:

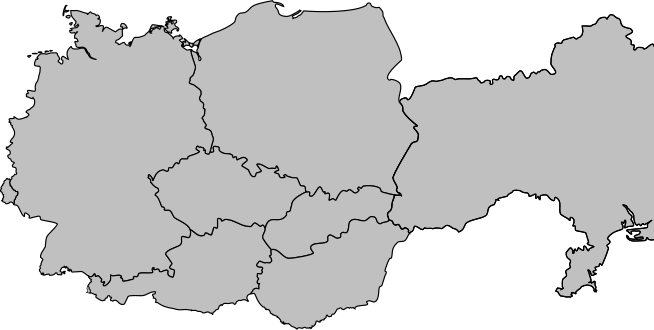
Is it possible to color this map with 3 colors so that no bordering countries have the same color?

Write a Prolog program that can answer this question.

9. Crosswords

Suppose that we'd like to fill in a 3 x 3 grid with letters so that every row and column contains one of these words:

AGE, AGO, CAN, CAR, NEW, RAN, ROW, WON

Write a Prolog program that can find all possible solutions.

10. Mini-Minesweeper

Consider the following tiny Minesweeper board of dimensions 5 x 2:

A number N means that there are N mines in adjacent squares (which may be adjacent horizontally or diagonally).

Write a Prolog program that can find all possible positions for the mines.

11. Occupations and Instruments

Write a Prolog program that can solve the following puzzle.

Kate, Maria and Roman have distinct occupations and play distinct musical instruments. Their occupations are doctor, lawyer, and teacher, and the instruments they play are piano, flute, and violin. Also:

1. Maria lives next to the doctor.

2. The lawyer plays the piano.

3. Maria is not the teacher.

4. Kate is a patient of the violinist.

Who plays the flute?