Introduction to Algorithms, 2021-2
Week 12: Notes

Some of this week's topics are covered in Problem Solving with Algorithms:

And in Introduction to Algorithms:

Here are some additional notes.

binary heaps

In the previous lecture, we introduced an abstract data type called a priority queue with these operations:

q.add(value)
Add a value to a priority queue.
q.is_empty()
Return true if the queue is empty.
q.remove_smallest()
Remove the largest value from a priority queue and return it.
A binary heap is a data structure that can efficiently implement a priority queue. Specifically, it has the form of a binary tree that satisfies two properties:

  1. Every node is smaller than its children. To be more precise, if a node with value p has a child with value c, then p < c. This is sometimes called the heap property.

  2. All levels of the tree are complete except possibly the last level, which may be missing some nodes on the right side.

For example, here is a binary heap:

This heap looks like a complete binary tree with one node missing on the right in the last level.

The height of a binary heap with N nodes is ⌊log2(N)⌋ = O(log N). In other words, a binary heap is always balanced.

We don’t store a binary heap using dynamically allocated nodes and pointers. Instead, we use an array, which is more compact, and is possible because of the shape of the binary heap tree structure. The binary heap above can be stored in an array like this:

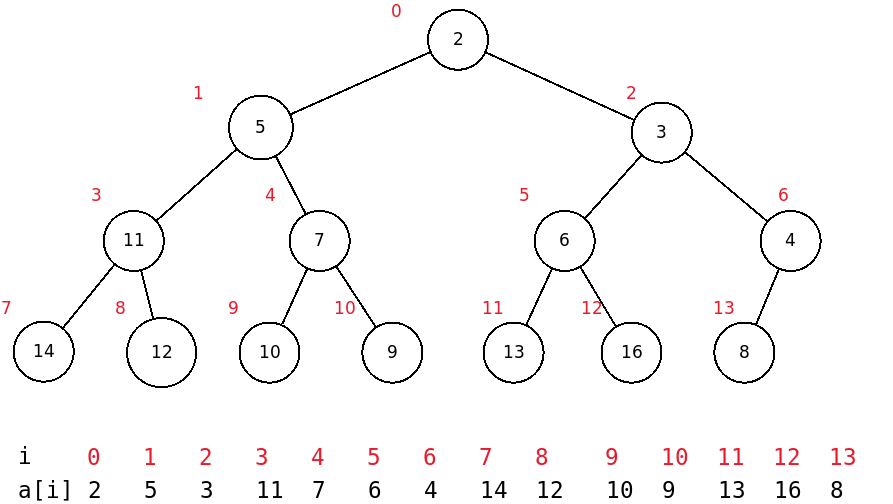
Notice that the array values are in the same order in which they appear in the tree, reading across tree levels from top to bottom and left to right.

From the tree above we can see the following patterns. If a heap node N has index i, then

In Python, we can store heap elements in an ordinary Python list (which, as we know, is actually a dynamically sizeable array):

class BinaryHeap:
    def __init__(self):
        self.a = []    # list will hold heap elements

Let's write helper functions that move between related tree nodes, using the formulas we saw above:

def left(i):
    return 2 * i + 1
    
def right(i):
    return 2 * i + 2
    
def parent(i):
    return ((i - 1) // 2

The heap depicted above is a min-heap, which supports a remove_smallest() operation. If we like, we may trivially modify it to be a max-heap, which instead supports a remove_largest() operation. In a max-heap, every node has a value that is larger than its children, and the largest value is at the top.

heap operations

We will now describe operations that will let us use a min-heap as a priority queue.

We first consider inserting a value v into a heap. To do this, we first add v to the end of the heap array, expanding the array size by 1. Now v is in a new leaf node at the end of the last heap level. The heap still has a valid shape, except that it may be invalid since one node (the node we just added) may have a value v that is smaller than its parent.

So we now perform an operation called up heap, which will move v upward if necessary to restore the heap properties. Suppose that v’s parent has value p, and p > v. That parent may have a second child with value w. We begin by swapping the values v and p. Now v’s children are p and w (if present). We know that v < p. If w is present then p < w, so v < w by transitivity. Thus the heap properties have been restored for the node that now contains v. And now we continue this process, swapping v upward in the heap until it reaches a position where it is not larger than its parent, or until it reaches the root of the tree.

In Python, the insert operation will look like this:

    # in class BinaryHeap

    def up_heap(self, i):
        while i > 0:
            p = parent(i)
            if self.a[p] <= self.a[i]:
                break
            self.a[i], self.a[p] = self.a[p], self.a[i]
            i = p

    def insert(self, x):
        self.a.append(x)
        self.up_heap(len(self.a) – 1)

The worst-case running time of an up heap operation is O(log N), since it will travel through O(log N) nodes at most (i.e. up to the top of the tree), and performs O(1) work at each step. And so insert() also runs in O(log N) in the worst case.

Now we consider removing the smallest value from a min-heap. Since the smallest value in such a heap is always in the root node, we must place some other value there. So we take the value at the end of the heap array and place it in the root, decreasing the array size by 1 as we do so. Now the heap still has a valid shape, however it may be invalid since its value at the root may be larger than one or both of its children.

So we now perform an operation called down heap on this value v, which will lower it to a valid position in the tree. If v is larger than one or both of its children, then let w be the value of the smallest of v's children. Then we know that v > w. We swap v with w. Now w's children are v and possibly some other value x. We know that w < v, and if there is another child x then w < x, since w was the smallest child. So the heap property has been restored for the node that now contains w. We then continue this process, swapping v downward as many times as necessary until v reaches a point where it has no larger children. The process is guaranteed to terminate successfully, since if v eventually descends to a leaf node there will be no children and the condition will be satisfied.

I won't provide Python code here for the down_heap() or remove_smallest() operations, but writing these is an excellent exercise.

heapifying an array

Suppose that we have an array a of numbers in any order, and we'd like to heapify the array, i.e. rearrange its elements so that they form a valid binary heap. How can we do this?

One possible approach would to iterate over the array elements from left to right, performing an up heap operation on each one. After each such operation, the array elements visited so far will be a valid binary heap, so when we are done we will have a valid heap containing all array elements. If there are N elements in the array, the total running time will be at most N · O(log N) = O(N log N).

However, there is a better way. We can instead iterate over the array elements from right to left, performing a down heap operation on each one. At each step, the heap property will be valid for all nodes that we've already visited, so when we're done will have a complete valid binary heap.

How long will this take? Suppose that there are N elements in the array. For simplicity, let's assume that N = 2k – 1 for some k, so that the heap has the form of a complete binary tree with height (k - 1). Then there are 2k – 1 leaves, which is approximately N / 2. We don't even need to perform a down heap operation on these, since there is nothing below them. There are 2k – 2 parents of leaves, which is approximately (N / 4). The down heap operation on each of these will take only one step, since each such node will fall at one most position. So the total running time will be proportional to

0 · (N / 2) + 1 · (N / 4) + 2 · (N / 8) + 3 · (N / 16) + …

Let's rewrite the expression above in a two-dimensional form:

N / 4 + N / 8 + N / 16 + N / 32 + N / 64 + …
      + N / 8 + N / 16 + N / 32 + N / 64 + …
               + N / 16 + N / 32 + N / 64 + … 
                       + N / 32 + N / 64 + …

                        + …

The sum of the first row above is N / 2. The sum of the second row is N / 4, and so on. The total of all rows is

N / 2 + N / 4 + N / 8 + … = N

Thus the total cost of this heapification process is O(N). It is remarkably efficient.

heapsort

We’ve already seen several sorting algorithms in this course: bubble sort, selection sort, insertion sort, merge sort and quicksort. We can use a binary heap to implement yet another sorting algorithm: heapsort. The essence of heapsort is simple: given a array of numbers to sort, we put them into a heap, and then we pull out the numbers one by one in sorted order.

Let’s examine these steps in a more detail. For heapsort, we want a max-heap, which lets us remove the largest element by calling a method remove_largest. Given an array of N values, we first heapify it as described above. After that, sorting the array is easy: we repeatedly call remove_largest to remove the largest element, which we place at the end of the array. In Python code, it might look like this:

class BinaryHeap:
    def __init__(self, a):
        self.a = a
        self.heapify()
    … 

def heapsort(a):
    heap = BinaryHeap(a)

    for i in range(len(a) - 1, 0, -1):   # n – 1, n – 2, …, 1
        a[i] = heap.remove_largest()

The total time for heapsort to sort N values is (a) the time to heapify the array plus (b) the time to remove each of the N values from the heap in turn. This is

O(N) + O(N log N) = O(N log N)

Thus heapsort has the same asymptotic running time as merge sort and quicksort. Some advantages of heapsort are that it runs on an array in place (unlike merge sort) and that it is guaranteed to run in time O(N log N) for any input (unlike quicksort).

representing graphs

A graph consists of a set of vertices (sometimes called nodes in computer science) and edges. Each edge connects two vertices. In a undirected graph, edges have no direction: two vertices are either connected by an edge or they are not. In a directed graph, each edge has a direction: it points from one vertex to another. A graph is dense if it has many edges relative to its number of vertices, and sparse if it has few such edges.

Graphs are fundamental in computer science. Many problems can be expressed in terms of graphs, and we can answer lots of interesting questions using various graph algorithms.

Generally we will assume that a graph with V vertices has vertex ids which are integers from 0 through (V - 1). Here is one such undirected graph:

How may we store a graph with V vertices in memory? As one possibility, we can use adjacency-matrix representation. The graph will be stored as a two-dimensional array g of booleans, with dimensions V x V. In Python, g will be a list of lists. In this representation, g[i][j] is true if and only there is an edge from vertex i to vertex j.

If the graph is undirected, then the adjacency matrix will be symmetric: g[i][j] = g[j][i] for all i and j.

Here is an adjacency-matrix representation of the undirected graph above. Notice that it is symmetric:

graph = [
    [False, True,  True,  False, False, True,  True],
    [True,  False, False, False, False, False, False],
    [True,  False, False, False, False, False, False],
    [False, False, False, False, True,  True,  False],
    [False, False, False, True,  False, True,  True],
    [True,  False, False, True,  True,  False, False],
    [True,  False, False, False, True,  False, False]
]

Alternatively, we can use adjacency-list representation, in which for each vertex we store an adjacency list, i.e. a list of its adjacent vertices. In Python this will take the form of a list of lists of integers. For a graph g, g[i] is the adjacency list of i, i.e. a list of ids of vertices adjacent to i. (If the graph is directed, then more specifically g[i] is a list of vertices to which there are edges leading from i.)

When we store an undirected graph in adjacency-list representation, then if there is an edge from u to v we store u in v’s adjacency list and also store v in u’s adjacency list.

Here is an adjacency-list representation of the undirected graph above:

graph = [
    [1, 2, 5, 6],    # neighbors of 0
    [0],             # neighbors of 1
    [0],             # …
    [4, 5],
    [3, 5, 6],
    [0, 3, 4],
    [0, 4]
]

Adjacency-matrix representation allows us to immediately tell whether two vertices are connected, but it may take O(V) time to enumerate a given vertex’s edges. On the other hand, adjacency-list representation is more compact for sparse graphs. With this representation, if a vertex has e edges then we can enumerate them in time O(e), but determining whether two vertices are connected may take time O(e), where e is the number of edges of either vertex. Thus, the running time of some algorithms may differ depending on which representation we use.

In this course we will usually represent graphs using adjacency-list representation.

depth-first search

In this course we will study two fundamental algorithms that can search a directed or undirected graph, i.e. explore it by visiting its nodes in some order.

The first of these algorithms is depth-first search, which is something like exploring a maze by walking through it. Informally, it works like this. We start at any vertex, and begin walking along edges. As we do so, we remember all vertices that we have ever visited. We will never follow an edge that leads to an already visited vertex. Each time we hit a dead end, we walk back to the previous vertex, and try the next edge from that vertex (as always, ignoring edges that lead to visited vertices). If we have already explored all edges from that vertex, we walk back to the vertex before that, and so on.

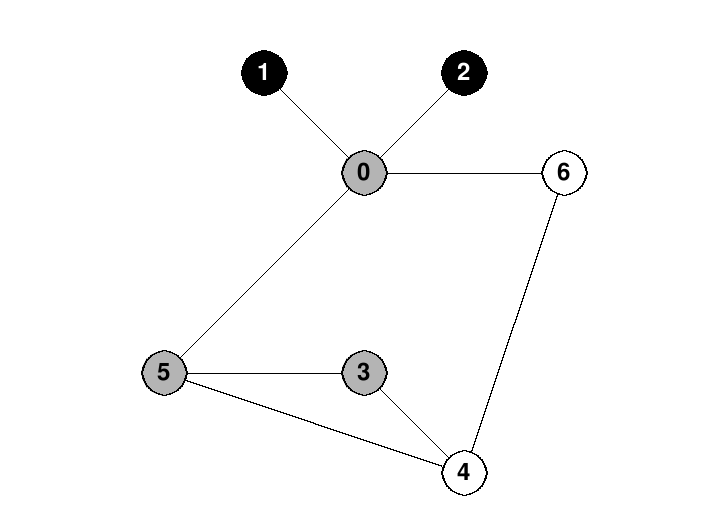
For example, consider the undirected graph that we saw above:

Suppose that we perform a depth-first search of this graph, starting with vertex 0. We might first walk to vertex 1, which is a dead end. The we backtrack to 0 and walk to vertex 2, which is also a dead end. Now we backtrack to 0 again and walk to vertex 5. From there we might proceed to vertex 3, then 4. From 4 we cannot walk to 5, since we have been there before. So we walk to vertex 6. From 6 we can't proceed to 0, since we have been there before. So we backtrack to 4, then back to 3, 5, and then 0. The depth-first search is complete, since there are no more edges that lead to unvisited vertices.

As a depth-first search runs, we may imagine that at each moment every one of its vertices is in three possible states:

Often when we draw pictures of a depth-first search (and also of some other graph algorithms), we draw unexplored vertices in white, frontier vertices in gray and explored vertices in black. For example, here is a picture of a depth-first search in progress on the graph above. The search started at vertex 0, and has just arrived at vertex 3:

Here's a larger graph, with vertices representing countries in Europe:

Here's a picture of a depth-first search in progress on this graph, using the same coloring scheme. The search started with Austria, and has now reached Italy:

implementing a depth-first search

It is easy to implement a depth-first search using a recursive function. In fact we have already done so in this course! For example, we wrote a function to add up all values in a binary tree, like this:

def sum(n):
    if n == None:
        return 0
    return sum(n.left) + n.val + sum(n.right)

This function actually visits all tree nodes using a depth-first tree search.

For a depth-first search on arbitrary graphs which may not be trees, we must avoid walking through a cycle in an infinite loop. To accomplish this, as described above, when we first visit a vertex we mark it as visited. Whenever we follow an edge, if it leads to a visited vertex then we ignore it.

If a graph has vertices numbered from 0 to (V – 1), we may efficiently represent the visited set using an array of V boolean values. Each value in this array is True if the corresponding vertex has been visited.

Here is Python code that implements a depth-first search using a nested recursive function. It takes a graph g in adjacency-list representation, plus a vertex id 'start' where the search should begin. It assumes that vertices are numbered from 0 to (V – 1), where V is the total number of vertices.

# recursive depth-first search
def dfs(g, start):
    visited = [False] * len(g)

    def visit(v):
        print('visiting', v)
        visited[v] = True
        for w in g[v]:           # for all neighbors of vertex v
            if not visited[w]:
                visit(w)

    visit(start)

This function merely prints out the visited nodes. But we can modify it to perform useful tasks. For example, to determine whether a graph is connected, we can run a depth-first search and then check whether the search visited every node. As we will see in later lectures and in Programming 2, a depth-first search is also a useful building block for other graph algorithms: determining whether a graph is cyclic, topological sorting, discovering strongly connnected components and so on.

A depth-first search does a constant amount of work for each vertex (making a recursive call) and for each edge (following the edge and checking whether the vertex it points to has been visited). So it runs in time O(V + E), where V and E are the numbers of vertices and edges in the graph.