Since we'll be using recursion in some new ways in this lecture, let's warm up by solving an exercise using recursion. Suppose that we'd like to write a function that builds a linked list containing the integers 1 through N, in ascending order.
Here is a Node class for a linked list:
class Node:
def __init__(self, val, next):
self.val = val
self.next = nextAs we've seen before, we can build a list iteratively by prepending values:
def list_to(n):
n = None
for i in range(n, 0, -1): # n, n - 1, ..., 1
n = Node(i, n) # prepend i to list
return nWe must loop over integers in reverse order, since we want to prepend n first and prepend 1 at the very end.
How can we write list_to() recursively? At first it may not be obvious how to do this. In the base case (when n == 0) we can return None. But in the recursive case, if we call list_to(n – 1) recursively we will get a list of integers from 1 to (n – 1). If we want to append n to that list, we'll have to walk down to the end of it, which will take O(n) time; we don't want that.
When we call ourselves recursively, it would be more useful to get back a list containing the integers 2 through n. Then we could simply prepend 1. However, list_to() cannot make a list like this.
This is one of many recursive problems in which we need to generalize the problem in order to solve it recursively. Consider this more general problem: we'd like to write a function list_from_to(a, b) that returns a linked list containing the values a through b. Certainly if we can write list_from_to(), then we can write list_to() trivially. And fortunately we can easily write list_from_to() recursively. Here is our solution:
def list_from_to(a, b):
# base case
if b < a:
return None
# recursive case
l = list_from_to(a + 1, b)
return Node(a, l) # prepend a to l
def list_to(n):
return list_from_to(1, n)We can solve many problems by using recursion to explore an exponential space.
As a first example of this technique, let's write a function that takes an integer n and prints out all strings of length n containing only characters from the set {'a', 'b', 'c'}. For example, if n = 2 then we will print these strings:
aa ab ac ba bb bc ca cb cc
And if n = 3:
aaa aab aac aba abb abc aca acb acc baa bab bac …
There will be 3n strings in the output list. That's because there are 3 possible choices for the first letter, 3 for the second letter, and so on for each of the n letters.
Any algorithm to generate these strings will surely take exponential time, since the length of the output is exponential in n. This is a sign that we will probably need to use recursion to solve this problem, since a set of loops without recursion will generally run in polynomial, not exponential, time.
We can solve this and many other recursive problems using either a top-down or bottom-up approach. In either approach, we use recursion to explore a space of possibilities. In the top-down approach, we build up a solution as we descend the tree. In the bottom-up approach, we return a solution at the leaves and extend it as the recursion unwinds. Let's first look at a top-down solution for this 'abc' problem.
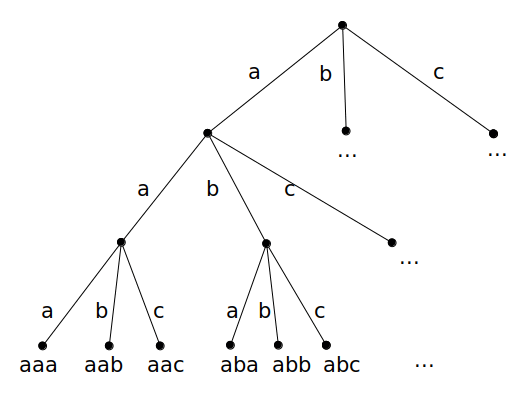
We can imagine a tree of choices that we must make as we choose a string to print out:

At each step, we choose the letter 'a', 'b' or 'c'. Affter we have made N choices, we have a string that we can print. In the picture above n = 3.
We can recurisvely explore this tree of choices. As the recursion descends, we will build up a string, appending a character at each step. At each leaf we will print out the string we have built. Here is our solution:
def abc(n, s = ''):
if n == 0:
print(s)
else:
for c in 'abc':
abc(n - 1, s + c)In a top-down solution, instead of appending to a string we may wish to save all the choices we have made so that they are available when we reach a leaf. As one possibility, we can save them in an array. Here is a solution to 'abc' that uses this approach:
def abc(n):
a = n * [ None ]
def choose(i):
if i == n: # we have chosen n letters
print(''.join(a)) # join them into a string
else:
for c in 'abc':
s[i] = c # choose s[i]
choose(i + 1) # recurse
choose(0)Now let's look at a bottom-up solution to this problem. We may notice its recursive structure. Specifically, consider the list of output strings for n = 3:
aaa aab aac aba abb abc ...
If we look at only the last two characters of each string, we see the strings aa, ab, ac, ba and so on, which is precisely the list of strings for n = 2. In other words, each string for n = 3 consists of a character 'a', 'b', or 'c' followed by some string generated by the same function with n = 2. This observation will allow us to write this function recursively.
Let's choose a base case that is as small as possible, i.e. n = 0. In this case should the function return an empty list, or a list with a single element? For a clue to the answer, recall that there should be 3n output strings. Of course 30 = 1, so this suggests that we should return a list of length 1. Indeed, there is exactly one string of length 0 containing only characters from the set {'a', 'b', 'c'}, namely the empty string.
Here is a recursive bottom-up solution:
def abc(n):
# base case
if n == 0:
return ['']
# recursive case
l = []
for c in 'abc':
for s in abc(n - 1):
l.append(c + s)
return lAlternatively, we may use a list comprehension to achieve the same result:
def abc(n):
if n == 0:
return ['']
return [c + s for c in 'abc' for s in abc(n - 1)]As we will see, we can use recursion to solve many similar combinatorial problems, such as finding all permutations or combinations of a list, all subsets of a set, and so on. For many such problems, either a top-down or bottom-up approach is possible. If your goal is only to print out a list of solutions, then the top-down approach is often adequate. If you want to write a function that actually returns a list of solutions, the bottom-up approach may be more appropriate.
As a second example of a combinatorial problem, let's consider the problem of generating all compositions of an integer. A composition of an integer N is a series of positive integers that add up to N. Order matters: (1 + 3) and (3 + 1) are distinct compositions of 4.
Here are all the compositions of 4:
1 + 1 + 1 + 1 1 + 1 + 2 1 + 2 + 1 1 + 3 2 + 1 + 1 2 + 2 3 + 1 4
Once again, we can imagine that in generating a composition we are descending a tree of possible choices:

Here is a top-down solution that prints out a composition at each leaf:
def compositions(n, s = ''):
if n == 0:
print(s)
else:
for i in range(1, n + 1):
compositions(n - i, s + str(i) + ' ')In the recursive call, we pass (n – i) because any composition of n consists of a first integer i followed by a composition of (n – i). This is the recursive structure of the problem.
Our function works:
>>> compositions(4) 1 1 1 1 1 1 2 1 2 1 1 3 2 1 1 2 2 3 1 4
Let's also look at a bottom-up solution to this problem. In
this approach, we'd
like to write a function that returns a list of compositions, where
each composition is itself a list of integers. In the base case, we
will return [[]] because there exists
one
composition of 0, namely the empty set. In the recursive case, we may
combine any choice i with any composition of (n – i). Here is our
solution:
def compositions(n):
if n == 0:
return [[]]
else:
return [[i] + l for i in range(1, n + 1) for l in compositions(n - i)]As a final example of a combinatorial problem, let's write a function that outputs all permutations of a string.
For example, if the input string is 'abc', the output will include these values:
abc acb bac bca cab cba
If the input string is 'abcd', the output will begin with these values:
abcd abdc acbd acdb adbc adcb bacd badc bcad …
If the length of the input string is N, then there will be N! output values, since there are N! permutations of a list of length N.
Once again, either a top-down or bottom-up solution is possible. We will write a top-down solution here.
We first need to understand the recursive structure of the problem. Look at the permutations of 'abcd' above. Notice that the first 6 permutations consist of the character 'a' plus some permutation of 'bcd'. The next 6 permutations consist of the character 'b' plus some permutation of 'acd', and so on. We see that to generate a permutation of a string s, we must first choose some first character c. Then we can generate the remainder of the permutation, which will be any permutation of (s – c), i.e. the string obtained by deleting c from s.
def permutations(s, t = ''):
if s == '':
print(t)
else:
for i in range(len(s)):
permutations(s[: i] + s[i + 1 :], t + s[i])It's also possible to write a bottom-up solution that returns a list of permutations of a string. You may wish to attempt this as an exercise.