Some of this week's topics are covered in Problem Solving with Algorithms:
In the last lecture we learned about depth-first search and breadth-first search, which are fundamental algorithms. In that lecture we used these algorithms to explore graphs. However these algorithms are more broadly applicable: we can use them to solve many problems in which we search through a state space. These problems have a graph-like structure. In each such problem, there is an initial state and a function that maps each state to a list of its possible successor states. We are searching for some path that leads from the initial state to a goal state.
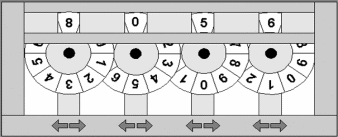
For example, consider the following device:

There are four wheels, each of which turn left and right. At every moment, the device displays a four-digit number at the top.
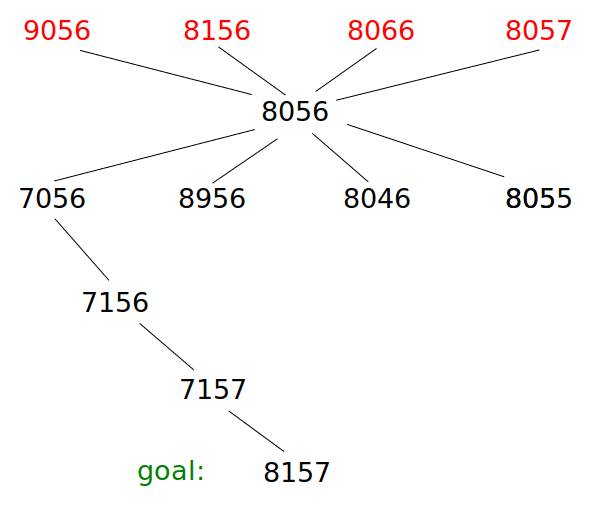
Consider the following problem. Initially the device displays 8056. In each move, we turn one of the wheels left or right by one position. Our goal is to reach the position 8157 using the smallest possible number of moves. However, we may not pass through the positions 8057, 8066, 8156, or 9056, which are forbidden.
This is a state space search problem. We can think of the state space as an abstract graph. Each state is a vertex of the graph, and there is an edge from each state to each of its successors. In this problem this abstract graph has 10,000 vertices. Every vertex has degree 8, since each state has 8 possible successors because each move turns one of 4 wheels in one of 2 directions. Here is a picture of a small subset of this graph, with the forbidden states in red:
Let's write a function wheel_dist() to solve this problem in general: given a start position, a goal position and a list of forbidden positions it will find the shortest possible path from the start to the goal. We will use a breadth-first search, since we want the shortest possible path and a depth-first search cannot find that.
We must first choose a representation for states. Various representations are possible: for example, we could represent the state 8056 by an integer, or by the list [8, 0, 5, 6], or the tuple (8, 0, 5, 6), or by the string '8056'. We will choose the last of these possibilities: each state will be a string of digits.
Let's first write a function that can generate a list of successor states of each state:
def successors(state):
ret = []
for wheel in range(4):
for dir in [1, -1]:
digit = (int(state[wheel]) + dir) % 10
ret.append(state[:wheel] + str(digit) + state[wheel + 1:])
return retNow we can write the main wheel_dist() function. It looks very much like our previous implementation of breadth-first search, but we call the successors() function in place of examining a concrete graph in memory. In this function we use a dictionary 'dist' that maps each state to its distance from the start state. We don't need a separate visited set, since the keys of 'dist' are exactly the states that we have visited:
def wheel_dist(start, goal, forbidden):
queue = deque()
dist = {}
queue.append(start)
dist[start] = 0
while len(queue) > 0:
s = queue.popleft()
for t in successors(s):
if t not in dist and t not in forbidden:
queue.append(t)
dist[t] = dist[s] + 1
return dist[goal]The function can easily solve our original problem:
>>> wheel_dist('8056', '8157', ['9056', '8156', '8066', '8057'])
4Arithmetic expressions are composed from numbers
and operators that act on those numbers. In this section we will use
the operators +, -, * and /,
the last of which denotes integer division.
In traditional mathematical notation, these
operators are infix operators: they are written between the values
that they act on (which are called operands). For example, we write 2
+ 2, or 8 - 7. In this last expression, 8 and 7
are the operands.
Here are some arithmetic expressions written using infix notation:
((4
+ 5) * (2 + 1))
((7
/ 2)
-
1)
We may choose an alternative syntax that uses
prefix notation, in which we write each operator before its
operands. For example, we write + 2 4 to mean the sum of
2 and 4, or / 8 2 to mean 8 divided by 2. Here are the
above expressions rewritten in prefix notation:
* + 4 5 + 2 1 - / 7 2 1
Or we may use postfix notation, in which operators come after
both operands: we might write 4 5 + to mean the sum of 4
and 5. Here are the above expressions in postfix notation:
4 5 + 2 1 + * 7 2 / 1 -
In infix notation we must write parentheses to distinguish
expressions that would otherwise be ambiguous. For example, 4 +
5 * 9 could mean either ((4 + 5) * 9) or (4
+ (5 * 9)). (Another way to disambiguate expressions is using
operator precedence. For example, * is generally
considered to have higher precedence than +. But in this
discussion we will assume that no such precedence exists.)
In prefix or postfix notation there is no need
either for parentheses or operator precedence, because expressions
are inherently unambiguous. For example, the prefix expression *
+ 4 5 9 is equivalent to ((4 + 5) * 9), and the
prefix expression + 4 * 5 9 is equivalent to (4 +
(5 * 9)). There is no danger of confusing these in prefix form
even without parentheses.
We may store expressions using an expression tree, which is a form of abstract syntax tree. An expression tree reflects an expression’s hierarchical structure. For example, here is an expression tree for the infix expression ((3 + 4) * (2 + 5)):
Note that this expression tree also corresponds to the prefix expression * + 3 4 + 2 5, or the postfix expression 3 4 + 2 5 + *. Equivalent expressions in infix, prefix or postfix form will always have the same tree! That’s because this tree reflects the abstract syntax of the expression, which is independent of concrete syntax which defines how expressions are written as strings of symbols.
We can easily store expression trees using objects in Python. Every interior node of the tree represents a binary operation, and every leaf is an integer. Here is a class for interior nodes:
class BinOp:
def __init__(self, left, op, right):
self.left = left
self.op = op
self.right = rightThis may remind you of the class for binary search trees that we saw a few weeks ago. However, note some important differences. In our representation of binary search trees, we held values (typically numbers) in every node, and the left and right children of every left node were None. In these expression trees, the leaves are Python integers.
We can build the expression tree in the picture above as follows:
l = BinOp(3, '+', 4) r = BinOp(2, '+', 5) top = BinOp(l, '*', r)
If we have an expression tree in memory, we may wish to evaluate it. To evaluate an expression means to determine its value. For example, when we evaluate the infix expression (2 + (3 * 4)), we get the value 14.
We first write a function that can apply an operator to two numbers:
def eval_op(x, op, y): if op == '+': return x + y if op == '-': return x - y if op == '*': return x * y if op == '/': return x // y assert False, 'unknown operator: ' + op
Now we can evaluate an expression tree with a straightforward recursive function:
def eval(e):
if isinstance(e, int):
return e
assert isinstance(e, BinOp)
l = eval(e.left)
r = eval(e.right)
return eval_op(l, e.op, r)Given an expression tree, it’s not hard to convert it to a string representation in either infix, prefix or postfix form. For example, we can generate a prefix expression as follows:
def to_prefix(e):
if isinstance(e, int):
return str(e)
l = to_prefix(e.left)
r = to_prefix(e.right)
return f'{e.op} {l} {r}'Or we may generate an infix expression from a tree:
def to_infix(e):
if isinstance(e, int):
return str(e)
l = to_infix(e.left)
r = to_infix(e.right)
return f'({l} {e.op} {r})'Notice that we fully parenthesize each subexpression in a generated infix expression. If we did not do this, then we might generate a string such as '3 + 4 * 5 + 2' when we really meant '((3 + 4) * (5 + 2))'. In a prefix expression, parentheses are unnecessary since prefix expressions are unambiguous.
Our discussion of expression syntax to this point has been somewhat informal. We will now formally define the syntax of arithmetic expressions, which will help us in the next section. For simplicity, we will assume that
all numbers consist of only a single digit
the only operators are +, -, *, / meaning integer addition, subtraction, multiplication and division
expressions have no embedded spaces
We can define the syntax of infix arithmetic expressions using the following context-free grammar:
digit → '0' | '1' |
'2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
op → '+' | '-' |
'*' | '/'
expr → digit | '(' expr op expr ')'
Context-free grammars are commonly used to define programming languages. A grammar contains non-terminal symbols (such as digit, op, expr) and terminal symbols (such as '0', '1', '2', …, '+', '-', '*', '/'), which are characters. A grammar contains a set of production rules that define how each non-terminal symbol can be constructed from other symbols. These rules collectively define which strings of terminal symbols are syntactically valid.
For example, ((4 + 5) * 9) is a valid
expression in the syntax defined by this grammar, because it can be
constructed from the top-level non-terminal expr by
successively replacing symbols using the production rules:
expr
→ (
expr op expr )
→ ( expr op digit )
→
(expr op 9)
→ (expr
* 9)
→ ((expr op expr) * 9)
→
((expr op digit) * 9)
→ ((expr
op 5) * 9)
→ ((expr + 5) *
9)
→ ((digit + 5) * 9)
→
((4 + 5) * 9)
You will learn more about context-free grammars in more advanced courses, but it’s worth taking this first look at them now because they are so commonly used to specify languages.
To modify our grammar to specify the syntax of prefix expressions, we need change only the last production rule above:
expr → digit | op expr expr
Or, for postfix expressions:
expr → digit | expr expr op
Note again that the prefix and postfix expression languages have no parentheses.
We would now like to parse arithmetic expressions defined by the grammar above. Given a string containing a prefix, infix, or postfix expression, we'd like to determine the expression's structure and (a) generate an expression tree or (b) evaluate the expression directly.
In our parsers we will need to read characters one at a time from a string. So let's first write a Reader class that lets us do that:
class Reader:
def __init__(self, s):
self.s = s.replace(' ', '') # ignore spaces
self.i = 0
def next(self):
c = self.s[self.i]
self.i += 1
return cIt works:
>>> r = Reader('+ 2 3')
>>> r.next()
'+'
>>> r.next()
'2'
>>> r.next()
'3'Let's write a function that can parse an arithmetic expression in prefix notation and generate an expression tree.
def parse_prefix(s):
reader = Reader(s)
def parse():
c = reader.next()
if c.isdigit():
return int(c)
assert c in '+-*/'
left = parse()
right = parse()
return BinOp(left, c, right)
return parse()
We can now parse an expression and evaluate it:
>>> e = parse_prefix('+ * 2 3 * 4 5')
>>> eval(e)
26Notice that the structure of the nested function parse() above follows the grammar rule for prefix expressions:
expr → digit | op expr expr
We have written a recursive-descent parser for an extremely simple language, i.e. the language of arithmetic expressions with operators +, -, *, / in prefix notation. Many interpreters and compilers for real programming languages such as Python also parse code using recursive-descent parsers, though of course those languages are far more complex.
If we wish to evaluate a prefix expression directly rather than generating a tree, we can do so by changing the last line of parse() above to
return eval_op(left, c, right)
Parsing an infix expression is not much more difficult. Recall the grammar rule for producing infix expressions:
expr → digit | '(' expr op expr ')'
We now write a recursive function that mirrors this rule:
def parse_infix(s):
reader = Reader(s)
def parse():
c = reader.next()
if c.isdigit():
return int(c)
assert c == '('
left = parse()
op = reader.next()
assert op in '+-*/'
right = parse()
assert reader.next() == ')'
return BinOp(left, op, right)
return parse()As with prefix expressions, we can make a trivial change to this function to evaluate an infix expression directly rather than generating a tree:
return eval_op(left, op, right)
To parse a postfix expression, we cannot easily use recursion. Instead, the most straightforward approach is to use a stack. As we read a postfix expression from left to right, each time we see a number we push it onto the stack. When we see an operator, we pop two numbers from the stack, apply the operator and then push the result back onto the stack. For example, in evaluating the postfix expression 4 5 + 2 1 + * we would perform the following operations:
push 4
push 5
pop 4 and 5, push 9
push 2
push 1
pop 2 and 1, push 3
pop 9 and 3, push 27
When we finish reading the expression, if it is valid then the stack will contain a single number, which is the result of our expression evaluation.
To generate a expression tree from a postfix expression, we can use a stack of pointers to expression trees. When we read an operand, we pop two subtrees from the stack, combine them into a BinOp object, then push it back on the stack.
In the tutorial we solved this exercise:
Consider a limping knight on a chessboard. On odd moves, it moves like a pawn, i.e. one square forward (or stays in place if it is at the top of the board). On even moves, it moves like a normal knight in chess. Write a function limping_dist(start, end) that returns the smallest number of moves that the knight must make to go from a given starting square to a given ending square. Assume that squares are pairs of coordinates, i.e. (1, 1) is the upper-left corner of the chessboard and (8, 8) is the lower-right corner.
This is a state space search problem. We'll represent each state by a tuple ((x, y), odd), where (x, y) is the knight's position and 'odd' is a boolean value that is True if the knight is about to make an odd move (i.e. move like a pawn).
from collections import deque
moves = [(2, 1), (2, -1), (1, 2), (1, -2), (-1, 2), (-1, -2), (-2, 1), (-2, -1)]
def successors(s):
(x, y), odd = s
if odd: # pawn move
return [((x, y - 1 if y > 1 else 1), False)]
else:
ret = []
for dx, dy in moves:
if 1 <= x + dx <= 8 and 1 <= y + dy <= 8:
ret.append( ((x + dx, y + dy), True) )
return ret
def limping_dist(start, goal):
queue = deque()
dist = {}
initial_state = (start, False)
queue.append(initial_state)
dist[initial_state] = 0
while len(queue) > 0:
s = queue.popleft()
for t in successors(s):
if t not in dist:
dist[t] = dist[s] + 1
if t[0] == goal:
return dist[t]
queue.append(t)
return -1 # unreachable