Write a non-recursive procedure that takes an integer N and writes out all subsets of { 1 .. N }.
A composition of a positive integer N is a sequence of positive integers that add up to N.
Write a method that takes an integer N and prints all its compositions. For example, if N = 4, the output could be
4 3 + 1 2 + 2 2 + 1 + 1 1 + 3 1 + 2 + 1 1 + 1 + 2 1 + 1 + 1 + 1
A partition of a positive integer N is a set of positive integers that add up to N.
Write a method that takes an integer N and prints all its partitions. For example, if N = 5, the output could be
5 4 + 1 3 + 2 3 + 1 + 1 2 + 2 + 1 2 + 1 + 1 + 1 1 + 1 + 1 + 1 + 1
Write a method combinations(int n, int k)
that prints out all k-element subsets of the set {1, 2, …, n}.
Is it possible to place 8 queens on a chessboard so that none of them attack each other? Write a C# program that can search for a solution and print it in this form:
. . Q . . . . . Q . . . . . . . . . . Q . . . . …
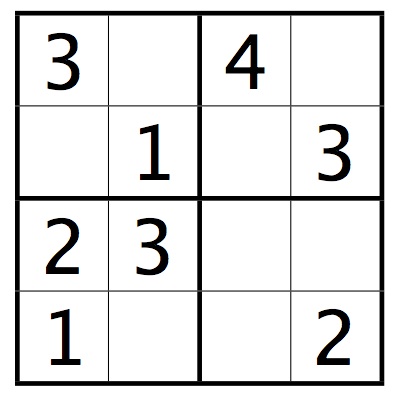
A mini-Sudoku puzzle looks like this:

To solve the puzzle, you must place a number from 1 to 4 in every square so that the numbers in every row, column, and mini-square are distinct.
Write a method that takes a mini-Sudoku puzzle as a 4 x 4 array of integers. Empty squares will be represented by the number 0. The method should return a solution to the puzzle (as a 4 x 4 array) if it can find one, otherwise null.