Assignment 4: Warlight

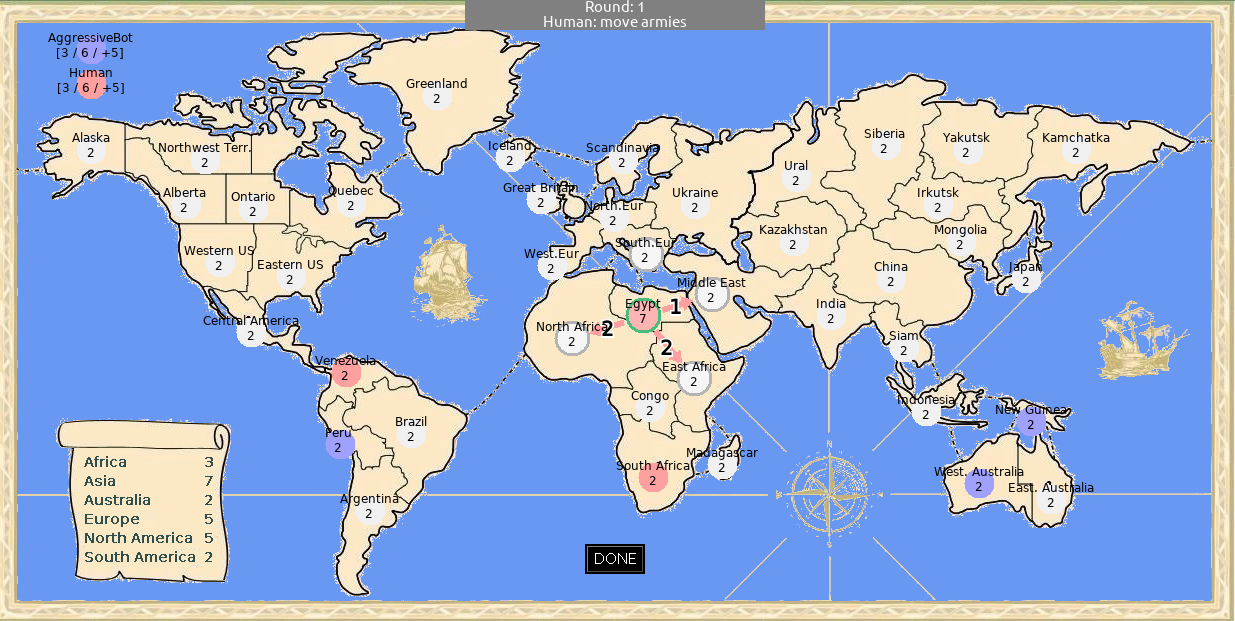
This assignment is worth 30 points and has three parts.

1. Base Strategy (10 pts)

Download the code from the Warlight repository on GitHub. Read the game rules on the GitHub page.

Warlight-Playground/src/MyBot.java contains a dummy bot that moves randomly. Improve this bot so that it can defeat the built-in AggressiveBot at least 80% of the time. You will want to use the Warlight API. Do not perform any state space searching at this point; we will implement that in the following sections.

I recommend developing MyBot incrementally. You can launch a game between MyBot and AggressiveBot with visualization enabled by running the main() method in MyBot.java. Watch the moves that MyBot makes. When you see it make a move that seems poor, update the code so that it will choose a better move next time around. By default, the game uses a random seed, so that every game is different. While you are working on your bot, you may wish to set a fixed seed so that the same random choices will occur in every game. To do that, add this line to runInternal() in MyBot.java:

config.game.seed = 0;   // use 0 or any other non-negative value as a fixed seed

To evaluate your bot, you can run a series of games between MyBot and AggressiveBot by running the main method in the WarlightFightConsole class. (In that method, uncomment the line "args = getTestArgs_1v1();" .)

Despite its fearsome-sounding name, AggressiveBot is actually pretty dumb, and you should be able to reach an 80% victory rate or higher without much difficulty.

2. Tree Search Algorithm (10 pts)

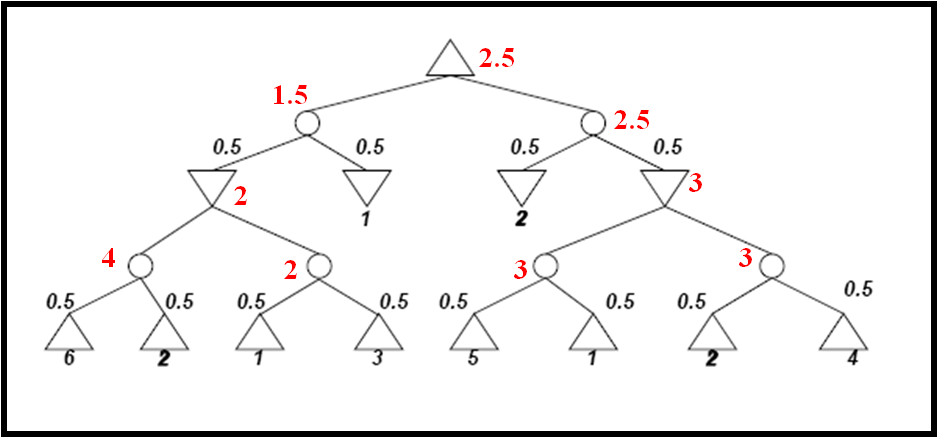
Implement either

First clone (or update your existing copy of) the ai_1 repository. Look in the minimax/src subdirectory, which has source files for the classes described in this section.

Write a general-purpose implementation that can search any game that implements the following interface:

// S = state type, A = action type
public interface Game<S, A> {
  S initialState();
  S clone(S state);
  int player(S state);         // which player moves next: 1 (maximizing) or 2 (minimizing)
  void apply(S state, A action);  // apply action to state, possibly with stochastic result
  boolean isDone(S state);     // true if game has finished
  double outcome(S state);     // 1.0 = player 1 wins, 0.5 = draw, 0.0 = player 2 wins
}

Your expectiminimax or MCTS class will implement this interface:

interface Strategy<S, A> {
  A action(S state);
}

A Strategy represents a strategy for playing a game. It is essentially a function which, given a state, decides what action the current player should take.

You must implement your algorithm so that it will work even if moves do not strictly alternate. For example, in some games player 1 might move twice, then player 2 might move twice, and so on. (Warlight is like this, since on each player's turn they have two moves: one to place armies and one to attack/transfer.)

expectiminimax

For expectiminimax, you will need these additional interfaces:

interface ActionGenerator<S, A> {
  List<A> actions(S state);  // actions to try in this state
}

class Possibility<S> {
  public double prob; // probability from 0..1
  public S state;
}

interface ResultGenerator<S, A> {
  List<Possibility<S>> possibleResults(S state, A action); // possible results of an action
}
public interface Evaluator<S> {
  double evaluate(S state);
}

The ActionGenerator and ResultGenerator interfaces exist because the Game interface does not have methods to return all possible actions at every state, or all possible results from any action. Such methods would be impractical, since Warlight's branching factor is so high. There may be many thousands of possible actions or results at any moment, and our algorithms cannot explore all of these. Instead, these interfaces are intended to return a small number of possible actions or results, chosen strategically and/or at random, as if the game's branching factor was much smaller. So these interfaces implement a (somewhat unfortunate) compromise to deal with the high branching factor.

Because these interfaces are separate from the main Game interface, you can test (for example) two strategy variants against each other that use two different ActionGenerators.

You should implement the following class in Expectiminimax.java:

class Expectiminimax<S, A> implements Strategy<S, A> {

  public Expectiminimax(Game<S, A> game,
                        ActionGenerator<S, A> actionGenerator,
                        ResultGenerator<S, A> resultGenerator,
                        Evaluator<S> evaluator, int limit) {
    …
  }     

}

In the Expectiminimax constructor:

Please implement alpha-beta pruning at least for max and min nodes in the search tree. You can optionally implement alpha-beta pruning even for chance nodes as described in section 5.5.1 of our text, but that is not required.

hints

Monte Carlo tree search

First, a word of warning: MCTS is a bit tricky to implement. Nevertheless it is an interesting algorithm, and you may attempt to implement it if you are up for the challenge.

You may want to follow the pseudocode of Algorithm 2 in this survey paper:

Cameron Browne et al, "A Survey of Monte Carlo Tree Search Methods" (2012)

The following paper is more approachable and may also be useful, though its pseudocode is less precise:

Mark Winands, Monte-Carlo Tree Search in Board Games (2016)

Your MCTS implementation will use the ActionGenerator and ResultGenerator interfaces described in the expectiminimax section above. Implement the following class in Mcts.java:

// Monte Carlo tree search
class Mcts<S, A> implements Strategy<S, A> {

  public Mcts(Game<S, A> game, Strategy<S, A> base,
              ActionGenerator<S, A> actionGenerator, ResultGenerator<S, A> resultGenerator,
              int limit) {
    …
  } 
}

In the Mcts constructor:

hints

    When performing backpropagation, do not use Algorithm 3 "UCT backup for two players" from the Browne paper, which is appropriate only for a negamax tree. (You could alternatively implement a negamax tree, but it may not be a great fit for this assignment since moves may not be strictly alternating.)

    1. Create chance nodes in the MCTS tree as described (briefly) in the Winands paper. Minimax nodes and chance nodes will alternate in the tree. As you traverse down the tree during the selection phase, each time you encounter a chance node you must choose a child node representing one possible stochastic outcome. Try to balance these choices so that the number of visits to each child node is proportional to the probability of the outcome it represents.

    2. Use determinization (mentioned in section 4.8.1 in the Browne paper). Create a separate MCTS tree for each determinization, making sure that all trees have the same top-level set of actions. You can think of each determinization as a non-stochastic world in which the pseudo-random result of any action is known in advance to both players. Run the algorithm in these trees in round-robin fashion, moving to a new tree on each iteration. After these runs have completed, each determinization will have values N (number of simulations) and Q (total reward) for the nodes below each top-level action. Combine the results from all determinizations in some way to determine a final action.

testing

The ai_1 repository contains two simple games that implement the interfaces above: Tic-Tac-Toe and Pig. Each includes several sample strategies. The classes ExpectiminimaxTest and MctsTest will run your expectiminimax or MCTS implementation on these games. It would be wise to make sure you can pass these tests before tackling Warlight in the next section.

Note that Tic-Tac-Toe is not stochastic, but you can still play it with expectiminimax or MCTS - there is just one possible result of every action.

3. Tree Search in Warlight (10 pts)

Write a Warlight bot SearchBot that uses your expectiminimax or MCTS implementation to search through the Warlight state space.

You will need to do the following:

class WarlightGame implements Game<GameState, Action> {
  @Override
  public GameState initialState() {
    return new GameState();
  }

  ...
}

Once your bot is working, evaluate its performance. Can it defeat your original MyBot from part 1? Does it perform better against AggressiveBot than MyBot did? In other words, does the lookahead tree search give you any benefit?

In my experiments, I've found that my MCTS-based bot can defeat my base strategy bot 70-80% of the time when given 200 ms of thinking time per move. I'm using chance nodes in the MCTS tree (the first of the two stochastic options described above) and these parameters:

To receive credit for this part of the assignment, your SearchBot must be able to defeat AggressiveBot at least 80% of the time. (I have not set this threshold any higher than for part 1, since I recognize that it may be challenging to make your bot perform well, especially for expectiminimax.)

hints

You will probably want to experiment with various parameters of your implementation. For either search method (expectiminimax or MCTS), you may wish to experiment with

For expectiminimax, you can also tune

For MCTS, you may want to experiment with

If you have two variations of your strategy, you can test them versus each other either using the Runner class in the ai_1 repository, or by running WarlightFightConsole.

4. Warlight Tournament

All entries received before the deadline for this assignment will automatically entered into a tournament in which your bots will play each other. In the tournament, each bot will have up to 0.5 second to make each move. When I run the tournament I'll use a slightly higher hard limit such as 0.6 seconds, so don't worry about going a few milliseconds over 0.5 second. If a bot fails to respond in time, it will make no move that turn, but will not automatically lose the game. Each bot will play several games against every other bot, both as player 1 and as player 2.

I will accept only single-threaded bots since the focus of this class is algorithms, not multi-threaded programming.

Your tournament entry does not have to use a tree search! If your hand-coded bot performs better or you want to use some other algorithm, that is fine too.