Week 11: Exercises

1. Stair Climbing

A staircase has n steps from bottom to top. A person walks up the staircase, and can take up to m steps at a time. Write a function

int stairs(int n, int m)

that returns the number of different ways in which the person may climb the stairs.

2. Carrots and Parsley

We wish to plant a garden with N beds in a row, each containing either carrots or parsley. No two adjacent beds may contain parsley. Write a method int garden(int n) that returns the number of possible ways in which the garden can be planted.

3. Box Stacking

You are given a set of N boxes. Each box i has height h_i, width w_i and depth d_i. Write a program that determines the maximum possible height of any stack of boxes, assuming that you can place box b on box c only if w_b < w_c and h_b < h_c. You may not rotate the boxes in any way.

4. Longest Path

Consider the following representation for directed weighted graphs. This class represents edges:

class Edge {
  public int dest;  // destination
  public double weight;
}

We can represent a graph in adjacency-list representation by a jagged array of type Edge[][]. If g is an array of this type, then g[i] is a subarray of edges leading from the i-th vertex.

Write a method int[] longest(Edge[][] graph, int start, int end) that takes a directed acyclic graph and finds the longest weighted path from vertex start to vertex end. The method should return a list of vertices along the path, including start and end. If no path exists between the vertices, return null.

5. Graph Coloring

Write a method that takes a connected undirected graph G, represented as a jagged array. The method should determine whether it is possible to color the graph with three colors (red, green, blue) such that no two adjacent vertices have a same color. If it is, it should print out a valid coloring.

6. Longest Path II

Write a method that takes an undirected graph G (represented as a jagged array) with vertices numbered 1 .. N. The method should return the length of the longest path from vertex 1 to vertex N. A path cannot cannot contain the same vertex twice. No efficient algorithm is known for solving this problem, so you will need to perform an exhaustive search of all possible paths.

7. Mini-Sudoku

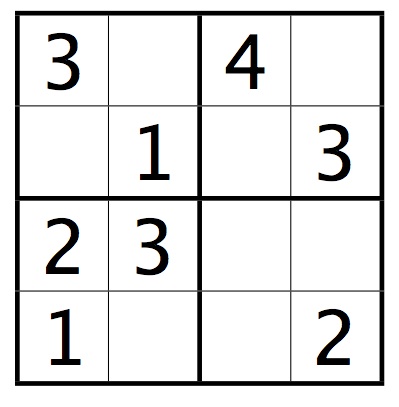
A mini-Sudoku puzzle looks like this:

To solve the puzzle, you must place a number from 1 to 4 in every square so that the numbers in every row, column, and mini-square are distinct.

Write a method that takes a mini-Sudoku puzzle as a 4 x 4 array of integers. Empty squares will be represented by the number 0. The method should return a solution to the puzzle (as a 4 x 4 array) if it can find one, otherwise null.