Assignment 4: Warlight

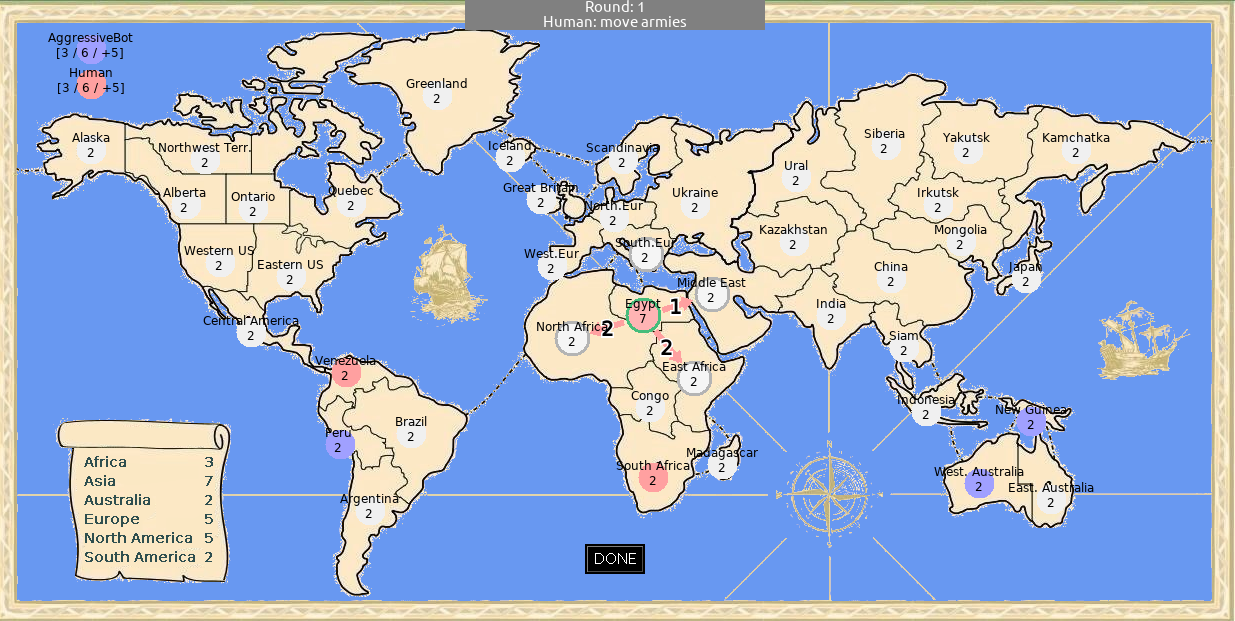
This assignment is worth 30 points (plus up to 5 bonus points) and has three parts.

1. Base Strategy (10 pts)

Download the Warlight code from the conquest-engine-gui repository. Read the game rules on the repository page.

The conquest.bot.playground package contains a class MyBot with a dummy bot that moves randomly. Improve this bot so that it can defeat the built-in AggressiveBot at least 70% of the time. You will want to use the Warlight API. Do not perform any state space searching at this point; we will implement that in the following sections.

To evaluate your bot, you can run a series of games between MyBot and AggressiveBot by running the main method in the ConquestFightConsole class. (In that method, uncomment the line "args = getTestArgs_1v1();" .)

The most straightforward way to improve MyBot is to use a rules-based approach. You might prefer certain continents when choosing initial territories, and you might prefer to place armies on frontier territories. You might also choose only to perform attacks that have a good chance of success.

Alternatively, you could use an optimization-based approach. You could write an evaluation function that judges a given board position based on factors such as the number of armies, territories and continents that each player has. And then you could examine all possible moves whenever your bot needs to place or move armies, and choose the move that will lead to a board position with the highest expected score. (This is, however, a bit trickier.)

2. Tree Search Algorithm (10 pts + up to 5 bonus pts)

Implement either the expectiminimax algorithm (inclulding alpha-beta pruning) or Monte Carlo tree search (MCTS) in Java. (I will award 5 bonus points if you successfully implement MCTS.)

Write an implementation that can search any game that implements the following interface:

// S = state type, A = action type
public interface Game<S, A> {
  S initialState();
  S clone(S state);
  int player(S state);         // which player moves next: 1 (maximizing) or 2 (minimizing)
  void apply(S state, A action);  // apply action to state, possibly with stochastic result
  boolean isDone(S state);     // true if game has finished
  double outcome(S state);     // 1.0 = player 1 wins, 0.5 = draw, 0.0 = player 2 wins
}

Your expectiminimax or MCTS class will implement this interface:

interface Strategy<S, A> {
  A action(S state);
}

A Strategy represents a strategy for playing a game. It is essentially a function which, given a state, decides what action the current player should take.

expectiminimax

For expectiminimax, you will need these additional classes/interfaces:

class Possibility<S> {
  public double prob; // probability from 0..1
  public S state;
}

interface Generator<S, A> {
  List<A> actions(S state);  // actions to try in this state
  List<Possibility<S>> possibleResults(S state, A action); // some possible results of an action
}

interface Evaluator<S> {
  double evaluate(S state);
}

Implement the following class:

class Expectiminimax<S, A> implements Strategy<S, A> {

  public Expectiminimax(Game<S, A> game, Generator<S, A> generator, Evaluator<S> evaluator,
                        int maxDepth) {
    …
  }     

}

In the Expectiminimax constructor:

Please implement alpha-beta pruning at least for max and min nodes in the search tree. You can optionally implement alpha-beta pruning even for chance nodes as described in section 5.5.1 of our text, but that is not required.

hints

Monte Carlo tree search

For Monte Carlo tree search, I suggest that you follow the pseudocode of Algorithm 2 in this excellent survey paper:

Browne, Cameron B., et al. "A survey of Monte Carlo tree search methods." IEEE Transactions on Computational Intelligence and AI in games 4.1 (2012): 1-43.

You will need this interface:

interface Generator<S, A> {
  List<A> actions(S state);  // actions to try in this state
}

Implement the following class:

// Monte Carlo tree search
class Mcts<S, A> implements Strategy<S, A> {

  public Mcts(Game<S, A> game, Generator<S, A> generator, Strategy<S, A> base,
              int determinizations, int timeLimit) {
    …
  } 
}

In the Mcts constructor:

hints

testing

Here are two simple games that implement the interfaces above. Each includes several sample strategies. You can use these for testing:

Here is a class that can run a series of games between two strategies to see which is better:

For example, you can run

Runner.play(new TicTacToe(), new BasicStrategy(), new TRandomStrategy(), 500);

and it will report

BasicStrategy won 448 (89.6%), 46 draws (9.2%), TRandomStrategy won 6 (1.2%)

Tug is a simple stochastic game. Your expectiminimax implementation should win against both TugStrategy and RandomStrategy at least 55% of the time, even with a search depth of only 1.

Tic-Tac-Toe is not stochastic, but you can still play it with expectiminimax. There is only one possible result of every action, so expectiminimax just becomes minimax. Your expectiminimax implementation should play evenly with BasicStrategy when the search depth is 2. As you increase the search depth, your implementation should do better and better. At a search depth of 10 (which will always search until the end of the game), you should never lose a game. Be sure to test both the case when you are player 1 (who moves first) and when you are player 2.

3. Tree Search in Warlight (10 pts)

Write a Warlight bot that uses your expectiminimax or MCTS implementation to search through the Warlight state space.

You will need to do the following:

class WarlightGame implements Game<GameState, Action> {
  @Override
  public GameState initialState() {
    return new GameState();
  }
        
  @Override
  public int player(GameState state) {
    return state.me;
  }
  ...
}
     class MyBot extends GameBot {

       // if using expectiminimax
       Expectiminimax<GameState, Action> strategy =
         new Expectiminimax<>(new WarlightGame(), new WarlightGenerator(), new WarlightEvaluator(), 1);
  
       // if using MCTS
       Mcts<GameState, Action> strategy =
         new Mcts<>(new WarlightGame(), new WarlightGenerator(), new BaseStrategy(), 10, 1000);

       ...

       @Override
       public ChooseCommand chooseRegion(List<Region> choosable, long timeout) {
         return (ChooseCommand) strategy.action(state);
       }

       ...
      }

Once your bot is working, evaluate its performance. Can it defeat your original MyBot from part 1? Does it perform better against AggressiveBot than MyBot did? In other words, does the lookahead tree search give you any benefit?

hints

Here are two possible ways to generate actions:

  1. Every action is a ChooseCommand, a PlaceAction or a MoveAction. With this approach, on each turn player 1 performs two actions (a PlaceAction followed by a MoveAction), and then player 2 performs two similar actions. So you will need to modify your expectiminimax or MCTS implementation so that actions do not necessarily alternate; instead, the player() method in the Game interface determines who will play next. Actually this is not so difficult: in a minimax (or negamax) tree a node can reasonably have child nodes representing actions by the same player, as long as the minimax implementation ensures that every node by player 1 is maximizing.

  2. Every action is a ChooseCommand or a PlaceMoveAction. A PlaceMoveAction is an entire move by one player, so this will allow you to use a traditional minimax tree in which player 1 and player 2 alternate. In your placeArmies() method, call your expectiminimax or MCTS implementation to generate a PlaceMoveAction. You will need to return this PlaceMoveAction's PlaceCommands from placeArmies(), and return its MoveCommands from a subsequent call to moveArmies(). You can do that by caching the PlaceMoveAction (or its MoveCommands) in your GameBot object until moveArmies() is called.

You will probably want to experiment with various parameters of your implementation. For either search method (expectiminimax or MCTS), you may wish to experiment with

For expectiminimax, you can also tune

For MCTS, you may want to experiment with

If you have two variations of your strategy, you can use the Runner class linked above to have them play each other. This will be faster than running ConquestFightConsole to make two bots play each other, since the bot mechanism in Warlight is complicated and slow, whereas the Runner class will access the forward model directly.

4. Warlight Tournament

All entries received before the soft deadline for this assignment will automatically entered into a tournament in which your bots will play each other. In the tournament, each bot will run in a virtual machine with a maximum heap size of 4 Gb and will have up to 3 seconds to make each move. When I run the tournament I'll use a slightly higher hard limit such as 3.1 seconds, so don't worry about going a few milliseconds over 3 seconds. If a bot fails to respond in time, it will make no move that turn, but will not automatically lose the game. Each bot will play several games against every other bot. I will have the bots switch sides after every game if possible.

I will accept only single-threaded bots since the focus of this class is algorithms, not multi-threaded programming.

Your tournament entry does not have to use a tree search! If your hand-coded bot performs better or you want to use some other algorithm, that is fine too. In your submission to me, if you have multiple bots then please indicate which one of them is tournament-worthy.