3.2Neural Networks
Artificial neural networks are inspired by the biological neural network. They
represent the powerful tool for solving or approximating problems, which are
difficult to solve in a traditional analytical way.
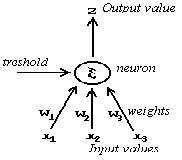
A neuron is an abstract device capable to compute the value of
a transfer function for any input in one computational step. Each neuron
has several connections representing either outputs of other neurons
or stimulus from the surroundings (neuron input values xi).
Every connection has associated a real number wi that indicates
the (synaptic) weight of the connection (i.e. its importance). Every neuron
has also value called threshold t. For a scheme of a formal
neuron see Fig. 3.2-1. The sum 
tells total stimulus, called neuron potential. Neuron responds to this
collected potential with the output response z=S(x),
where S is non-linear transfer function, usually of sigmoid form (e.g.
S(x)=1/(1+exp(-kx)) where k is constant representing the slope coefficient
of the transfer function.) If the potential is greater then threshold,
point x=[x1,x2,...] lies in the positive halfspace
defined by separating hyperplane x=0. Otherwise it lies in the complement
halfspace. This neuron facility enables classification of inputs into two
classes.
Figure 3.2-1: The basic structure of a formal neuron.
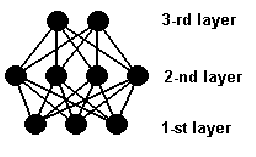
A neural network is a finite set of neurons (input neurons, output neurons
and other neurons), oriented interconnections among neurons (network topology),
weights and thresholds. A multi-layer neural network is a neural network
with a directed acyclic interconnection graph. Its set of neurons consists
of a sequence pairwise disjunctive subsets called layers. In the interconnection
graph, there are only edges from i-th to the (i+1)-th layer only. The first
layer (input layer) is the set of all input neurons and the last layer
(output layer) is the set of all output neurons of the network. For an
example of such a network see Fig. 3.2-2. The networks distinguish two
modes of work - adapting mode (network training) and active mode (network
recall):
-
Training: At first the user must create training a set. Training set
is set of input values and corresponding expected outputs. Then training
algorithm can start. The aim of the training algorithm is to find a set
of weights that ensures that for each input vector contained in the training
set the actual output vector produced by the network equals the desired
output vector.
-
Recall: Well-trained neural network is able to approximate the problem
it was trained for. It gives correct answers for all known inputs and is
able to approximate them in the unknown ones.
Figure 3.2-2: An example of a multi-layer neural network.
We decided to use neural networks for evaluating the genes when no analytical
function can be used. Trained neural network can compute the fitness function
value. Topology establishing and training is performed in separate system
component before genetic algorithm is started. Once trained, the network
configuration (topology, weights,...) can be saved in a file for further
use. The object representing neural network is created at the start of
the genetic algorithm computation. When running, the genetic algorithm calls
just one neural network method for gene evaluation.